题目内容
设函数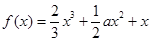 ,
,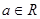 .
.
(Ⅰ)当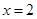 时,
时,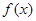 取得极值,求
取得极值,求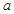 的值;
的值;
(Ⅱ)若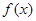 在
在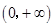 内为增函数,求
内为增函数,求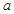 的取值范围.
的取值范围.
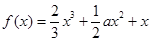 ,
,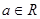 .
.(Ⅰ)当
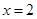 时,
时,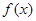 取得极值,求
取得极值,求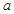 的值;
的值;(Ⅱ)若
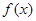 在
在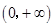 内为增函数,求
内为增函数,求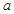 的取值范围.
的取值范围. (Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
本试题主要是考查导数的几何意义的运用以及导数求解函数的单调区间的极值的综合运用。
(1)由题意:
解得 .
.
(2)方程 的判别式
的判别式 ,根据判别式符号来证明得到。
,根据判别式符号来证明得到。
解: ,
,
(Ⅰ)由题意:
解得 . ………………3分
. ………………3分
(Ⅱ)方程 的判别式
的判别式 ,
,
(1) 当 , 即
, 即 时,
时, ,
,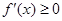 在
在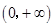 内恒成立, 此时
内恒成立, 此时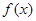 为增函数; ------ 6分
为增函数; ------ 6分
(2) 当 , 即
, 即 或
或 时,
时,
要使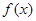 在
在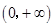 内为增函数, 只需在
内为增函数, 只需在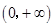 内有
内有 即可, 设
即可, 设 ,
,
由 得
得  , 所以
, 所以 .
.
由(1) (2)可知,若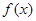 在
在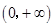 内为增函数,
内为增函数,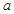 的取值范围是
的取值范围是 .---12分
.---12分
(1)由题意:

解得
 .
.(2)方程
 的判别式
的判别式 ,根据判别式符号来证明得到。
,根据判别式符号来证明得到。解:
 ,
, (Ⅰ)由题意:

解得
 . ………………3分
. ………………3分(Ⅱ)方程
 的判别式
的判别式 ,
,(1) 当
 , 即
, 即 时,
时, ,
,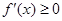 在
在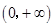 内恒成立, 此时
内恒成立, 此时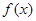 为增函数; ------ 6分
为增函数; ------ 6分(2) 当
 , 即
, 即 或
或 时,
时,要使
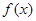 在
在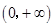 内为增函数, 只需在
内为增函数, 只需在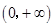 内有
内有 即可, 设
即可, 设 ,
,由
 得
得  , 所以
, 所以 .
. 由(1) (2)可知,若
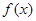 在
在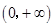 内为增函数,
内为增函数,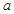 的取值范围是
的取值范围是 .---12分
.---12分
练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
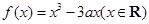 .
.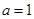 时,求
时,求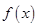 的极小值;
的极小值;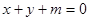 对任意的
对任意的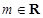 都不是曲线
都不是曲线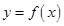 的切线,求
的切线,求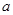 的取值范围.
的取值范围.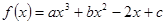 在
在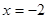 时有极大值6,在
时有极大值6,在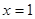 时有极小值,求
时有极小值,求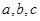 的值;并求
的值;并求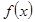 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.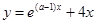 (
(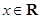 )有大于零的极值点,则实数
)有大于零的极值点,则实数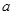 范围是 ( )
范围是 ( )



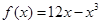 在区间
在区间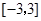 上的最小值是 .
上的最小值是 .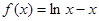 在区间
在区间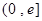 的最大值为( )
的最大值为( )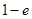
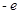
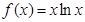 ,
,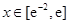 ,则
,则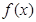 的最大值为____________,最小值为___________.
的最大值为____________,最小值为___________. ,(
,( ),
),
 与曲线
与曲线 在它们的交点(1,c)处具有公共切线,求a,b的值
在它们的交点(1,c)处具有公共切线,求a,b的值 时,若函数
时,若函数 的单调区间,并求其在区间(-∞,-1)上的最大值。
的单调区间,并求其在区间(-∞,-1)上的最大值。 是常数)在[-2,2]上有最大值3,那么在[-2,2]上的最小值是 ( ▲ )
是常数)在[-2,2]上有最大值3,那么在[-2,2]上的最小值是 ( ▲ )