Question

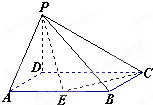（2012•姜堰市模拟）如图，四棱锥P-ABCD中，底面ABCD是矩形，PD⊥平面ABCD，且PD=AD=1，AB=2，点E是AB上一点，且二面角P-EC-D的平面角为

π

4

，求三棱锥B-PEC的体积．

Answer 1

分析：作DM⊥CE，垂足为M，连接PM，由三垂线定理得PM⊥CE，则∠PMD是二面角P-EC-D的平面角，再利用等体积计算三棱锥的体积．

解答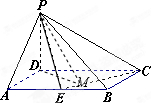：解：作DM⊥CE，垂足为M，连接PM，由三垂线定理得PM⊥CE
∴∠PMD是二面角P-EC-D的平面角．
∵二面角P-EC-D的平面角为

π

4

，∴∠PMD=

π

4

∵PD⊥平面ABCD，PD=1
∴DM=1
∵AB=DC=2，∴∠DCE=30°
∴∠BCE=60°，∴BE=

3

∴S△BEC=

1

2

×

3

×1=

3

2

∴V_B-PEC=V_P-BEC=

1

3

×

3

2

×1=

3

6

．

点评：本题以四棱锥为载体，考查面面角，考查三棱锥体积的计算，正确作出面面角是关键．