题目内容
17.已知函数(I)求函数![]() 的值域;
的值域;
(II)若对任意的![]() ,函数
,函数![]() ,
,![]() 的图象与直线
的图象与直线![]() 有且仅有两个不同的交点,试确定
有且仅有两个不同的交点,试确定![]() 的值(不必证明),并求函数
的值(不必证明),并求函数![]() 的单调增区间.
的单调增区间.
本小题主要考查三角函数公式,三角函数图象和性质等基础知识,考查综合运用三角函数有关知识的能力.
(Ⅰ)解:f(x)=![]()
=2![]()
=2sin![]()
由-1≤sin![]() ≤1,得-3≤2sin
≤1,得-3≤2sin![]() -1≤1.
-1≤1.
可知函数f(x)的值域为[-3,1].
(Ⅱ)解:由题设条件及三角函数图象和性质可知,y=f(x)的周期为π,又由![]() >0,得
>0,得![]() =π,即得
=π,即得
![]() =2.
=2.
于是有f(x)=2sin(2x-![]() )-1,再由2kπ-
)-1,再由2kπ-![]() ≤2x-
≤2x-![]() ≤2kπ+
≤2kπ+![]() (k
(k![]() Z),解得
Z),解得
kπ-![]() ≤x≤kπ+
≤x≤kπ+![]() ( k
( k![]() Z).
Z).
所以y=f(x)的的单调增区间为[kπ-![]() , kπ+
, kπ+![]() ]( k
]( k![]() Z).
Z).

练习册系列答案
相关题目
 (其中
(其中 )
) 的值域; (II)若对任意的
的值域; (II)若对任意的 ,函数
,函数 ,
, 的图象与直线
的图象与直线 有且仅有两个不同的交点,试确定
有且仅有两个不同的交点,试确定 的值(不必证明),并求函数
的值(不必证明),并求函数 的单调增区间
的单调增区间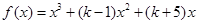 ,其中
,其中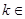
 .
. 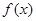 有三个不同零点,求
有三个不同零点,求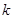 的取值范围;
的取值范围;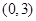 上不是单调函数,求
上不是单调函数,求 ,其中常数
,其中常数
 处取得极值,求a的值;
处取得极值,求a的值;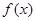 的单调递增区间;
的单调递增区间;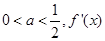 表示
表示 ,
, ,试比较
,试比较 的大小,并加以证明。
的大小,并加以证明。 (其中
(其中 )
) 的值域;
的值域;
 的图象与直线
的图象与直线 的两个相邻交点间的距离为
的两个相邻交点间的距离为 ,求函数
,求函数