题目内容
已知函数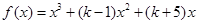 ,其中
,其中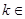
 .
.
(I)若函数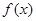 有三个不同零点,求
有三个不同零点,求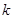 的取值范围;
的取值范围;
(II)若函数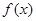 在区间
在区间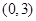 上不是单调函数,求
上不是单调函数,求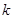 的取值范围.
的取值范围.
【答案】
(I)因为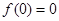 ,所以函数
,所以函数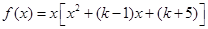 有三个不同零点的充要条件是关于
有三个不同零点的充要条件是关于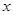 的方程
的方程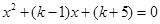 有两个不相等的非零实根,…1分
有两个不相等的非零实根,…1分
即 ,且
,且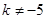 .
.
故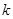 的取值范围是
的取值范围是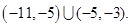 …………5分
…………5分
(II)解法一: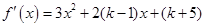 ,函数
,函数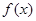 在区间
在区间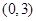 上不是单调函数的充要条件是关于
上不是单调函数的充要条件是关于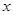 的方程
的方程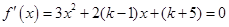 有两个不相等的实数根,且至少有一个实数根在区间
有两个不相等的实数根,且至少有一个实数根在区间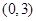 内. …………7分
内. …………7分
1.若 ,则
,则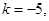
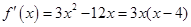 .
.
方程 的两个实根
的两个实根 均不在区间
均不在区间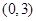 内,所以
内,所以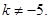 …………8分
…………8分
若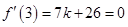 ,则
,则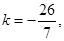
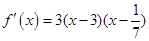 .
.
方程 在区间
在区间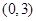 内有实根
内有实根 ,所以
,所以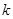 可以为
可以为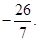 …………9分
…………9分
2.若方程 有一个实根在区间
有一个实根在区间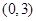 内,另一个实根在区间
内,另一个实根在区间 外,
外,
则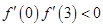 ,即
,即 …………10分
…………10分
3.若方程 在区间
在区间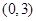 内有两个不相等的实根,则
内有两个不相等的实根,则
 ………11分
………11分
综合①②③④得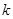 的取值范围是
的取值范围是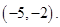 …………12分
…………12分
(II)解法二: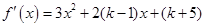 ,
,
函数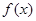 在区间
在区间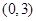 上不是单调函数的充要条件是关于
上不是单调函数的充要条件是关于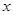 的方程
的方程
在区间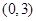 上有实根且
上有实根且 …………7分
…………7分
关于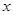 的方程
的方程 在区间
在区间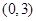 上有实根的充要条件是
上有实根的充要条件是
 使得
使得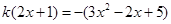 …………8分
…………8分
 使得
使得
令 有
有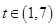 ,记
,记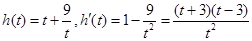
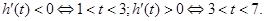 …………10分
…………10分
则函数 在
在 上单调递减,在
上单调递减,在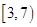 上单调递增,所以有
上单调递增,所以有
即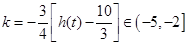 .…………11分
.…………11分
又由  得
得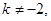 且
且
故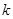 的取值范围是
的取值范围是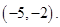 …………12分
…………12分
(II)解法三:记函数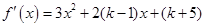 在区间
在区间 上的最大值为
上的最大值为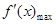 ,
,
最小值为 函数f(x)在区间
函数f(x)在区间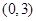 上不单调
上不单调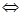 函数f(x)在区间
函数f(x)在区间 上不单调
上不单调
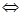
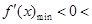
 …………7分
…………7分
因为函数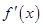 的图像是开口向上、对称轴为
的图像是开口向上、对称轴为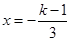 的抛物线,
的抛物线,
所以 ,
,
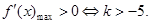 …………9分
…………9分
当 时,
时,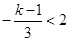 ,
,
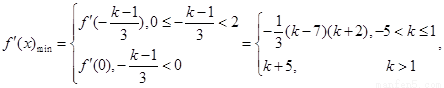 ……11分
……11分
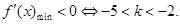 故
故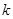 的取值范围是
的取值范围是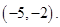
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目






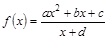 (其中
(其中 是实数常数,
是实数常数, )
) ,函数
,函数 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求 的值;
的值; ,总有
,总有 ,求
,求 的取值范围;
的取值范围; ,
, ,且对任意
,且对任意 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数 的取值范围.
的取值范围.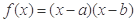 (其中
(其中 )的图象如图(上)所示,则函数
)的图象如图(上)所示,则函数 的图象是( )
的图象是( ) 
