题目内容
设点A为圆x2+y2=8上动点,点B(2,0),点O为原点,那么∠OAB的最大值为 .
分析:只证明当点A位于x轴的上方时,同理可证明当点A位于x轴的下方时的情况.当AB⊥x轴时,∠OAB取得最大值为45°.当AB⊥x轴时,把x=2代入圆的方程可得22+y2=8,解得y=2.可得∠OAB=45°.作Rt△OAB的外接圆C.可得⊙C与⊙O内切,即两圆只有唯一的一个公共点A(2,2).当点A取位于x轴的上方的其它位置A′时,连接OA′、BA′,交⊙C于点M,连接OM.得到∠OMB=∠OAB=45°>∠OA′B即可.
解答:解:只证明当点A位于x轴的上方时,同理可证明当点A位于x轴的下方时的情况.
当AB⊥x轴时,∠OAB取得最大值为45°.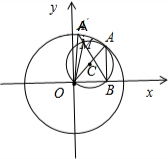
当AB⊥x轴时,把x=2代入圆的方程可得22+y2=8,解得y=2.
可得∠OAB=45°.
作Rt△OAB的外接圆C.
∵直径OA=2
=OC+
.
∴⊙C与⊙O内切,即两圆只有唯一的一个公共点A(2,2).
当点A取位于x轴的上方的其它位置A′时,连接OA′、BA′,交⊙C于点M,连接OM.
则∠OMB=∠OAB=45°>∠OA′B.
因此,∠OAB的最大值为45°.
故答案为:45°.
当AB⊥x轴时,∠OAB取得最大值为45°.

当AB⊥x轴时,把x=2代入圆的方程可得22+y2=8,解得y=2.
可得∠OAB=45°.
作Rt△OAB的外接圆C.
∵直径OA=2
| 2 |
| 2 |
∴⊙C与⊙O内切,即两圆只有唯一的一个公共点A(2,2).
当点A取位于x轴的上方的其它位置A′时,连接OA′、BA′,交⊙C于点M,连接OM.
则∠OMB=∠OAB=45°>∠OA′B.
因此,∠OAB的最大值为45°.
故答案为:45°.
点评:本题考查了三角形的外接圆、两圆内切、圆周角与圆外角的关系,属于难题.

练习册系列答案
相关题目
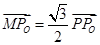 .
.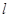 :y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.
:y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.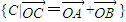 ⊆{(x,y)|x2+y2≤9},则实数t的最大值为 .
⊆{(x,y)|x2+y2≤9},则实数t的最大值为 .