题目内容
设点A在圆x2+y2=1内，点B（t，0），O为坐标原点，若集合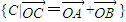
⊆{（x，y）|x2+y2≤9}，则实数t的最大值为 ．
【答案】分析：利用集合
⊆{（x，y）|x2+y2≤9}，结合向量的模长公式，即可得到结论．
解答：
解：∵集合
⊆{（x，y）|x2+y2≤9}，
∴
≤9
∵点A在圆x2+y2=1内，点B（t，0），
∴由向量的运算可得1+t2+2tcos∠AOB≤9
∴t2+2t-8≤0
∴-4≤t≤2
∴实数t的最大值为2
故答案为：2
点评：本题考查向量知识的运用，考查向量模长的计算，考查解不等式，属于中档题．
⊆{（x，y）|x2+y2≤9}，结合向量的模长公式，即可得到结论．解答：
解：∵集合⊆{（x，y）|x2+y2≤9}，∴
≤9∵点A在圆x2+y2=1内，点B（t，0），
∴由向量的运算可得1+t2+2tcos∠AOB≤9
∴t2+2t-8≤0
∴-4≤t≤2
∴实数t的最大值为2
故答案为：2
点评：本题考查向量知识的运用，考查向量模长的计算，考查解不等式，属于中档题．
练习册系列答案
相关题目
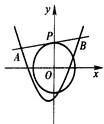设点P（m，n）在圆x2+y2=2上，l是过点P的圆的切线，切线l与函数y=x2+x+k（k∈R）的图象交于A，B两点，点O是坐标原点．