Question

【题目】在中，角的三条对边分别为，.

(1)求；

(2)点在边上，，，，求.

Answer 1

【答案】（1）；（2）2

【解析】

（1）由题意利用正弦定理与三角恒等变换求出sinB与cosB的关系，得出tanB的值，从而求出B的值；

（2）根据互补的两角正弦值相等，得到sin∠ADB＝sin∠ADC的值，再利用正弦、余弦定理求得AD、AC的值．

（1）由bcosCbsinC＝a，

利用正弦定理得：sinBcosCsinBsinC＝sinA，

即sinBcosCsinBsinC＝sinBcosC+cosBsinC，

得sinBsinC＝cosBsinC，

又C∈（0，π），所以sinC≠0，

所以sinB＝cosB，

得tanB，

又B∈（0，π），所以B；

（2）如图所示，

由cos∠ADC，∠ADC∈（0，π），

所以sin∠ADC，

由因为∠ADB＝π﹣∠ADC，

所以sin∠ADB＝sin∠ADC；

在△ABD中，由正弦定理得，，

且AB＝4，B，

所以AD；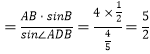

在△ACD中，由余弦定理得，

AC2＝AD2+DC2﹣2ADDCcos∠ADC

24，

解得AC＝2．