Question

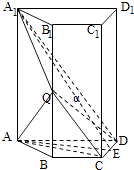
【题目】如图，四棱柱ABCD﹣A1B1C1D1中，A1A⊥底面ABCD，四边形ABCD为梯形，AD∥BC，且AD=2BC，过A1、C、D三点的平面记为α，BB1与α的交点为Q．

（1）证明：Q为BB1的中点；
（2）求此四棱柱被平面α所分成上下两部分的体积之比；
（3）若AA1=4，CD=2，梯形ABCD的面积为6，求平面α与底面ABCD所成二面角的大小．

Answer 1

【答案】
（1）证明：∵四棱柱ABCD﹣A1B1C1D1中，四边形ABCD为梯形，AD∥BC，

∴平面QBC∥平面A1D1DA，

∴平面A1CD与面QBC、平面A1D1DA的交线平行，∴QC∥A1D

∴△QBC∽△A1AD，

∴ = ，

∴Q为BB1的中点；

（2）解：连接QA，QD，设AA1=h，梯形ABCD的高为d，四棱柱被平面α所分成上、下两部分的体积为V1，V2，

设BC=a，则AD=2a，∴ = = ，VQ﹣ABCD= = ahd，

∴V2= ，

∵V棱柱= ahd，

∴V1= ahd，

∴四棱柱被平面α所分成上、下两部分的体积之比 ；

（3）解：在△ADC中，作AE⊥DC，垂足为E，连接A1E，则DE⊥平面AEA1，∴DE⊥A1E，

∴∠AEA1为平面α与底面ABCD所成二面角的平面角，

∵BC∥AD，AD=2BC，

∴S△ADC=2S△ABC，

∵梯形ABCD的面积为6，DC=2，

∴S△ADC=4，AE=4，

∴tan∠AEA1= =1，

∴∠AEA1= ，

∴平面α与底面ABCD所成二面角的大小为 ．

【解析】（1）证明平面QBC∥平面A1D1DA，可得△QBC∽△A1AD，即可证明Q为BB1的中点；（2）设BC=a，则AD=2a，则 = = ，VQ﹣ABCD= = ahd，利用V棱柱= ahd，即可求出此四棱柱被平面α所分成上、下两部分的体积之比；（3）△ADC中，作AE⊥DC，垂足为E，连接A1E，则DE⊥平面AEA1 ， DE⊥A1E，可得∠AEA1为平面α与底面ABCD所成二面角，求出S△ADC=4，AE=4，可得tan∠AEA1= =1，即可求平面α与底面ABCD所成二面角的大小．