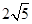题目内容
已知函数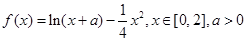 .
.
(Ⅰ)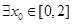 ,使得函数
,使得函数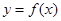 在
在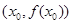 的切线斜率
的切线斜率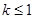 ,求实数
,求实数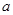 的取值范围;
的取值范围;
(Ⅱ)求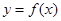 的最小值.
的最小值.
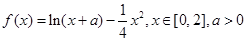 .
.(Ⅰ)
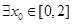 ,使得函数
,使得函数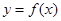 在
在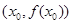 的切线斜率
的切线斜率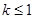 ,求实数
,求实数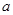 的取值范围;
的取值范围;(Ⅱ)求
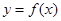 的最小值.
的最小值.(Ⅰ) (Ⅱ)
(Ⅱ)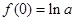
 (Ⅱ)
(Ⅱ)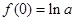
(Ⅰ)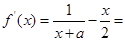
 ,由题意知,不等式
,由题意知,不等式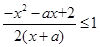 在
在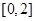 上有解,2分
上有解,2分
不等式等价变形为, ,记
,记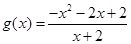 ,则
,则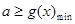 . 4分
. 4分
设
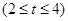 ,则
,则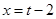 ,则有
,则有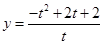
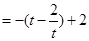 ,易知
,易知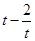 单调递增,故
单调递增,故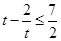 ,所以
,所以
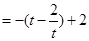
 ,故
,故 ,又因为
,又因为 即实数
即实数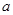 的取值范围的是
的取值范围的是 . 6分
. 6分
(Ⅱ)令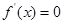 ,即
,即
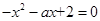 ,∵
,∵ ,∴方程的两个根为
,∴方程的两个根为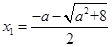 (舍去),
(舍去),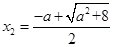 , 8分
, 8分
因为 ,则
,则 ,且当
,且当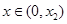 时,
时,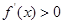 ;
;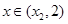 时,
时,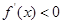 ,故函数可能在
,故函数可能在 或
或 处取得最小值,∵
处取得最小值,∵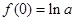 ,
,
 ,故当
,故当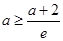 ,即
,即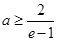 时,函数最小值为
时,函数最小值为 ;当
;当
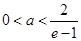 ,函数最小值为
,函数最小值为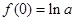 . 11分
. 11分
综上所述:当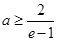 时,函数最小值为
时,函数最小值为 ;
;
当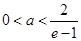 时,函数最小值为
时,函数最小值为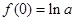 . 12分
. 12分
【命题意图】本题主要考查导数的几何意义和利用导数求函数的最值,意在考查运用数形结合思想的能力和运算求解能力.
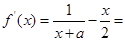
 ,由题意知,不等式
,由题意知,不等式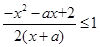 在
在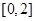 上有解,2分
上有解,2分不等式等价变形为,
 ,记
,记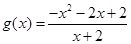 ,则
,则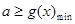 . 4分
. 4分设

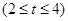 ,则
,则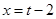 ,则有
,则有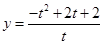
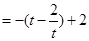 ,易知
,易知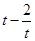 单调递增,故
单调递增,故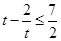 ,所以
,所以
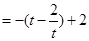
 ,故
,故 ,又因为
,又因为 即实数
即实数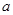 的取值范围的是
的取值范围的是 . 6分
. 6分(Ⅱ)令
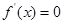 ,即
,即
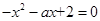 ,∵
,∵ ,∴方程的两个根为
,∴方程的两个根为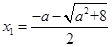 (舍去),
(舍去),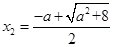 , 8分
, 8分因为
 ,则
,则 ,且当
,且当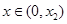 时,
时,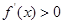 ;
;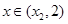 时,
时,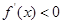 ,故函数可能在
,故函数可能在 或
或 处取得最小值,∵
处取得最小值,∵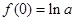 ,
,
 ,故当
,故当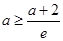 ,即
,即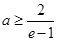 时,函数最小值为
时,函数最小值为 ;当
;当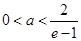 ,函数最小值为
,函数最小值为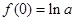 . 11分
. 11分综上所述:当
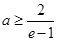 时,函数最小值为
时,函数最小值为 ;
;当
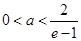 时,函数最小值为
时,函数最小值为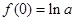 . 12分
. 12分【命题意图】本题主要考查导数的几何意义和利用导数求函数的最值,意在考查运用数形结合思想的能力和运算求解能力.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
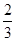 时,求函数y=f(x)的单调区间与极值.
时,求函数y=f(x)的单调区间与极值.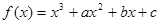 有两个极值点
有两个极值点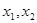 ,若
,若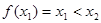 ,则关于
,则关于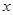 的方程
的方程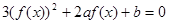 的不同实根个数为 ( )
的不同实根个数为 ( )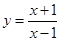 在点(3,2)处的切线与直线
在点(3,2)处的切线与直线 垂直,则
垂直,则

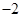


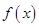 的极大值和极小值
的极大值和极小值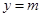 与函数
与函数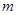 的范围
的范围 的导函数为
的导函数为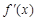 ,那么下列说法正确的是( )
,那么下列说法正确的是( )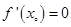 ,则
,则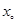 是函数
是函数 的极值点
的极值点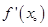 可能不存在
可能不存在 .
. 时,求函数
时,求函数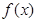 值域;
值域;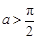 时,求函数
时,求函数 的单调区间.
的单调区间. 上的点到直线
上的点到直线 的最短距离是( )
的最短距离是( )