Question

设{a_n}为等比数列,公比为q.

(1)已知a₁+a₃=10,a₄+a₆=,求a_n.

(2)已知a₁·a₉=64,a₃+a₇=20,求a₁₁.

   

Answer 1

思路分析：用基本量来表示已知条件,建立a₁,q的方程组,找到a₁,q的值即可进一步求解,此法称为基本量法.

    解:(1)由已知得

得q³=,∴q=.∴a₁=8.

∴a_n=a₁·q^n-1=8×()^n-1=2^4-n.

(2)由已知得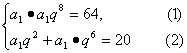

    由②式可知a₁＞0,那么①式可化简为

a₁q⁴=8.                           ③

    由于q≠0,得=.

    解得q²=或2.

    代入③式,当q²=时,可得a₁=32,a₁₁=q₁q¹⁰=1.

    当q²=2时,a₁=2,a₁₁=a₁q¹⁰=64.

    综上,a₁₁=64或1.