题目内容
8.化简$\frac{\sqrt{1-2sin39°cos39°}}{sin39°-cos39°}$=-1.分析 由正弦、余弦函数的性质判断出sin39°<cos39°,由平方关系化简所求的式子可得答案.
解答 解:因为sin39°<cos39°,
所以$\frac{\sqrt{1-2sin39°cos39°}}{sin39°-cos39°}$=$\frac{\sqrt{si{n}^{2}39°-2sin39°cos39°+co{s}^{2}39°}}{sin39°-cos39°}$
=$\frac{\sqrt{(sin39°-cos39°)^{2}}}{sin39°-cos39°}$=$\frac{|sin39°-cos39°|}{sin39°-cos39°}$=$\frac{-(sin39°-cos39°)}{sin39°-cos39°}$=-1,
故答案为:-1.
点评 本题考查同角三角函数的基本关系,正弦、余弦函数的性质,注意化简前后的符号.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
18.体育测试成绩分别为四个等级,优、良、中、不及格,某班55名学生参加测试的结果如表:
(1)从该班任意抽取1名学生,求该名学生的测试成绩为“良”或“中”的概率;
(2)测试成绩为“优”的3名男生记为a1,a2,a3,2名女生的成绩记为b1,b2,现从这5人中任选2人参加学校的某项体育比赛,求参赛学生中恰有一名女生的概率.
| 等级 | 优 | 良 | 中 | 不及格 |
| 人数 | 5 | 21 | 24 | 5 |
(2)测试成绩为“优”的3名男生记为a1,a2,a3,2名女生的成绩记为b1,b2,现从这5人中任选2人参加学校的某项体育比赛,求参赛学生中恰有一名女生的概率.
19.椭圆y2+$\frac{{x}^{2}}{{m}^{2}}$=1(0<m<1)上存在点P使得PF1⊥PF2,则m的取值范围是( )
| A. | [$\frac{\sqrt{2}}{2}$,1) | B. | (0,$\frac{\sqrt{2}}{2}$] | C. | [$\frac{1}{2}$,1) | D. | (0,$\frac{1}{2}$] |
18.随着杜会的发展,大多数家庭的经济状况不断提高,可是膏少年的身体健康指标却每况愈下,该观象备受杜会人士的关注,某一网站线上调查结果显示,青少年身体健康不达标的主要原因有以下三项:“饮食不规律造成营养不均衡”,“学业任务繁重”,“缺乏锻炼”,据统计,60名学生参加调查的情况如下表所示:
(1)现从这60名学生中按照参加调查的项数分层抽取6名学生进行了解情况,医疗部分决定在这已抽取的6名学生中随机抽取2名进行体检,记这2名学生中参加调查的项数为3的学生人数为ξ,求ξ的分布列和数学期望;
(2)医疗部分对部分学生一周内进行体育锻炼的时间x(单位:小时)和身体健康指标y进行了一定的统计分析,得到如下数据
由表中数据,求得线性回归方程为y=0.8x+a,若某学生一周内进行体育锻炼的时间x=12,求该学生的身体健康指标值.
| 参加调查的项数 | 0 | 1 | 2 | 3 |
| 所占比例 | $\frac{1}{6}$ | P | $\frac{1}{3}$ | $\frac{1}{3}$ |
(2)医疗部分对部分学生一周内进行体育锻炼的时间x(单位:小时)和身体健康指标y进行了一定的统计分析,得到如下数据
| 一周内进行体育锻炼的时间 | 4 | 6 | 8 | 10 |
| 身体健康指标 | 3 | 5 | 6 | 8 |
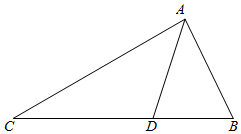 如图,在△ABC中,AC=16,∠C=$\frac{π}{6}$,点D在BC边上,且BD=6$\sqrt{3}$,tan∠ADB=$\frac{2\sqrt{3}}{3}$.
如图,在△ABC中,AC=16,∠C=$\frac{π}{6}$,点D在BC边上,且BD=6$\sqrt{3}$,tan∠ADB=$\frac{2\sqrt{3}}{3}$.