题目内容
在直角坐标系内，满足不等式x2-y2≥0的点(x,y)的集合(用阴影表示)是…………（ ）
B.
解析试题分析：由x2-y2≥0得：
，即
或
，再有线性规划的方法画出即可。
考点：本题考查二元一次不等式（组）与平面区域．
点评：本题主要应用转化思想把二元二次不等式表示的平面区域转化为一元二次不等式组表示的平面区域。．
练习册系列答案
相关题目
若实数
满足
则
的最小值是（ ）
| A．-1 | B．0 | C． | D．2 |
设变量
满足约束条件
则目标函数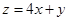
的最大值为（ ）
| A．4 | B．11 | C．12 | D．14 |
已知实数
满足
则
的最小值等于
| A．0 | B．1 | C．2 | D．3 |
设函数
，则满足
的x的取值范围是
A． ，2] | B．[0，2] | C．[1，+ ） | D．[0，+） |
若不等式组
表示的平面区域是一个直角三角形，则该直角三角形的面积是（ ）
A． | B． | C． | D．或 |
在直角坐标系中，满足不等式
的点
的集合（用阴影表示）是（ ）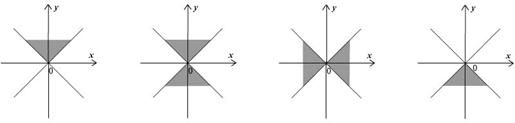 
| A． | B． | C． | D． |
已知变量x.y满足约束条件
,则f(x,y)＝
的取值范围是( )
A．( , ) | B．(,＋∞) | C．[,] | D．(－∞,) |
在平面直角坐标系中，若不等式组
表示的平面区域为面积为16，那么z＝2x－y的最大值与最小值的差为（ ）
| A．8 | B．10 | C．12 | D．16 |