题目内容
已知椭圆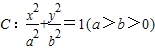 的长轴长为4.
的长轴长为4.(1)若以原点为圆心、椭圆短半轴为半径的圆与直线y=x+2相切,求椭圆焦点坐标;
(2)若点P是椭圆C上的任意一点,过原点的直线L与椭圆相交于M,N两点,记直线PM,PN的斜率分别为kPM,kPN,当
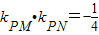 时,求椭圆的方程.
时,求椭圆的方程.
【答案】分析:(1)由 ,再结合椭圆的长轴的长为4,进而根据椭圆中a,b,c的关系得到焦点的坐标.
,再结合椭圆的长轴的长为4,进而根据椭圆中a,b,c的关系得到焦点的坐标.
(2)由题意可设M(x,y),N(-x,-y),P(x,y),所以有 ,两式相减得:
,两式相减得: ,再结合两条直线的斜率与题中条件可得答案.
,再结合两条直线的斜率与题中条件可得答案.
解答:解:(1)由 …(2分)
…(2分)
又因为2a=4,
所以a=2,又a2=4,b2=2…(4分)
所以c2=a2-b2=2,
∴ …(6分)
…(6分)
(2)由于过原点的直线L与椭圆相交的两点M,N交于坐标原点对称
不妨设:M(x,y),N(-x,-y),P(x,y)
因为M,N,P在椭圆上,
所以它们满足椭圆方程,即有
两式相减得: .…(8分)
.…(8分)
由题意它们的斜率存在,则 …(10分)
…(10分)

故所求椭圆的方程为 …(12分)
…(12分)
点评:本题主要考查了椭圆的标准方程,涉及了椭圆与直线的位置关系,以及直线的斜率等问题,综合性强.
 ,再结合椭圆的长轴的长为4,进而根据椭圆中a,b,c的关系得到焦点的坐标.
,再结合椭圆的长轴的长为4,进而根据椭圆中a,b,c的关系得到焦点的坐标.(2)由题意可设M(x,y),N(-x,-y),P(x,y),所以有
 ,两式相减得:
,两式相减得: ,再结合两条直线的斜率与题中条件可得答案.
,再结合两条直线的斜率与题中条件可得答案.解答:解:(1)由
 …(2分)
…(2分)又因为2a=4,
所以a=2,又a2=4,b2=2…(4分)
所以c2=a2-b2=2,
∴
 …(6分)
…(6分)(2)由于过原点的直线L与椭圆相交的两点M,N交于坐标原点对称
不妨设:M(x,y),N(-x,-y),P(x,y)
因为M,N,P在椭圆上,
所以它们满足椭圆方程,即有

两式相减得:
 .…(8分)
.…(8分)由题意它们的斜率存在,则
 …(10分)
…(10分)
故所求椭圆的方程为
 …(12分)
…(12分)点评:本题主要考查了椭圆的标准方程,涉及了椭圆与直线的位置关系,以及直线的斜率等问题,综合性强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

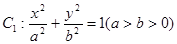 的长轴长为4,离心率为
的长轴长为4,离心率为 ,
, 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点 ,且与直线
,且与直线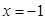 相切.
相切.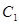 的方程;
(ⅱ)求动圆圆心
的方程;
(ⅱ)求动圆圆心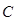 的轨迹方程;
的轨迹方程; ,椭圆
,椭圆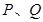 ,满足
,满足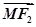 与
与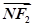 共线,
共线,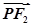 与
与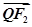 共线,且
共线,且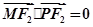 ,求四边形
,求四边形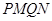 面积的最小值.
面积的最小值.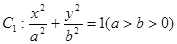 的长轴长为4,离心率为
的长轴长为4,离心率为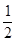 ,
, 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点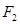 ,且与直线
,且与直线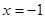 相切.
相切. 的方程; (ⅱ)求动圆圆心
的方程; (ⅱ)求动圆圆心 轨迹的方程;
轨迹的方程;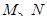 ,椭圆
,椭圆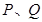 ,满足
,满足 与
与 共线,
共线,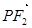 与
与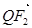 共线,且
共线,且 ,求四边形
,求四边形 面积的最小值.
面积的最小值.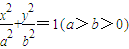 的长轴长为4,且点
的长轴长为4,且点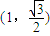 在该椭圆上.
在该椭圆上.