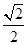题目内容
某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )
A. | B.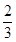 cm3 cm3 | C. cm3 cm3 | D.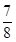 cm3 cm3 |
D
解析试题分析:观察三视图可知,该几何体是棱长为1的正方体去掉一个三棱柱,底面为直角三角形,直角边长为 ,所以此多面体的体积是
,所以此多面体的体积是 =
=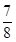 ,故选D。
,故选D。
考点:本题主要考查三视图及几何体体积计算。
点评:简单题,必考类型的题目,正确认识几何体特征是关键。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
在长方体ABCD—A1B1C1D1中,有( )条棱所在的直线与直线AA1是异面直线且互相垂直。
| A.2 | B.4 | C.6 | D.8 |
已知某个几何体的三视图如右图,根据图中标出的尺寸(单位: cm),可得这个几何体的体积是( )
A. cm3 cm3 | B. cm3 cm3 |
C. cm3 cm3 | D.2 cm3 |
下列判断正确的是( )
| A.棱柱中只能有两个面可以互相平行 |
| B.底面是正方形的直四棱柱是正四棱柱 |
| C.底面是正六边形的棱台是正六棱台 |
| D.底面是正方形的四棱锥是正四棱锥 |
下列说法正确的是( )
| A.有两个面平行,其余各面都是四边形的几何体叫棱柱. |
| B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱. |
| C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥. |
| D.棱台各侧棱的延长线交于一点. |
若某几何体的三视图如图1所示,则此几何体的表面积是( )
A. | B. | C. | D. |
经过空间任意三点作平面( )
| A.只有一个 | B.可作二个 |
| C.可作无数多个 | D.只有一个或有无数多个 |
已知四棱锥 的三视图如图所示,则四棱锥
的三视图如图所示,则四棱锥 的四个侧面中面积最大的是
的四个侧面中面积最大的是
A. | B. | C. | D. |
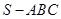 的所有顶点都在球
的所有顶点都在球 的球面上,
的球面上, 是边长为
是边长为 的正三角形,
的正三角形, 为球
为球 ,则此棱锥的体积为( )
,则此棱锥的体积为( )