题目内容
下列说法正确的是( )
| A.有两个面平行,其余各面都是四边形的几何体叫棱柱. |
| B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱. |
| C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥. |
| D.棱台各侧棱的延长线交于一点. |
D
解析试题分析: A.有两个面平行,其余各面都是四边形的几何体叫棱柱.不符合棱柱的定义,不正确;结合下图可知B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱.不正确;
棱锥有一个面是多边形,其余各面都是有一个公共顶点的三角形的几何体,故C不正确;
棱台是由棱锥截得的,故棱台各侧棱延长后要交与一点,故D正确,故选D。
考点:本题主要考查常见几何体的定义及特征。
点评:基础题,根据多面体的性质和几何体的定义来判断,采用举反例的方法加以判断。

练习册系列答案
相关题目
如图是一个几何体的正视图和侧视图。其俯视图是面积为 的矩形。则该几何体的体积是
的矩形。则该几何体的体积是
| A.8 | B. |
| C.16 | D. |
利用斜二测画法得到的
①三角形的直观图一定是三角形; ②正方形的直观图一定是菱形;
③等腰梯形的直观图可以是平行四边形; ④菱形的直观图一定是菱形.
以上结论正确的是 ( )
| A.①② | B.① | C.③④ | D.①②③④ |
某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )
A. | B.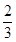 cm3 cm3 | C. cm3 cm3 | D.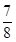 cm3 cm3 |
已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题:
①若m⊥α,m⊥β,则α∥β;
②若α⊥γ,β⊥α,则α∥β;
③若m∥α,n∥β,m∥n,则α∥β;
④若m、n是异面直线,m⊥α,m∥β,n⊥β,n∥α,则α⊥β
其中真命题是( )
| A.①和② | B.①和③ | C.③和④ | D.①和④ |
如图,三棱柱A1B1C1—ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( ).
| A.AE、B1C1为异面直线,且AE⊥B1C1 |
| B.AC⊥平面A1B1BA |
| C.CC1与B1E是异面直线 |
| D.A1C1∥平面AB1E |
( )如图,正四棱锥 的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是
的所有棱长相等,E为PC的中点,则异面直线BE与PA所成角的余弦值是
A. | B. | C. | D. |

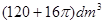



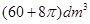
 。则该几何体的俯视图可以是( )
。则该几何体的俯视图可以是( )
