题目内容
10.设点P(x0,y0)是圆x2+y2=10上的任意一点,若直线x0x+y0y=a与此圆恒有交点,则实数a的取值范围是-10≤a≤10.分析 利用直线x0x+y0y=a与此圆恒有交点,可得$\frac{|a|}{\sqrt{{{x}_{0}}^{2}+{{y}_{0}}^{2}}}$$≤\sqrt{10}$,根据点P(x0,y0)是圆x2+y2=10上的任意一点,即可求出实数a的取值范围.
解答 解:由题意,x02+y02=10,
∵直线x0x+y0y=a与此圆恒有交点,
∴$\frac{|a|}{\sqrt{{{x}_{0}}^{2}+{{y}_{0}}^{2}}}$$≤\sqrt{10}$,
∴|a|≤10,
∴-10≤a≤10.
故答案为:-10≤a≤10.
点评 本题主要考查直线和圆的位置关系,点到直线的距离公式的应用,属于基础题.

练习册系列答案
相关题目
20.不等式|2x-1|≤7的解集是( )
| A. | {x|x≥-3} | B. | {x|x≤4} | C. | {x|-3≤x≤4} | D. | {x|x≤-3或x≥4} |
15.已知函数f(x)=e|x|+|x|-k有两个零点,则实数k的取值范围是( )
| A. | (0,1) | B. | (1,+∞) | C. | (-1,0) | D. | (-∞,-1) |
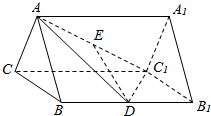 在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C是矩形,D、E分别是线段BB1、AC1的中点.
在三棱柱ABC-A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C是矩形,D、E分别是线段BB1、AC1的中点.