题目内容
15.已知函数f(x)=e|x|+|x|-k有两个零点,则实数k的取值范围是( )| A. | (0,1) | B. | (1,+∞) | C. | (-1,0) | D. | (-∞,-1) |
分析 由题意,k=e|x|+|x|,有两个交点,k=ex+x(x>0),有1个交点,构造g(x)=ex+x(x>0),可得g(x)>g(0)=1,即可得出结论.
解答 解:由题意,k=e|x|+|x|,有两个交点,
∴k=ex+x(x>0),有1个交点,
令g(x)=ex+x(x>0),则g′(x)=ex+1>0,
∴g(x)>g(0)=1,
∴k>1,
故选:B.
点评 本题主要考查函数的零点,考查学生分析解决问题的能力,正确转化是关键..

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
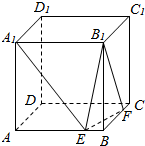 如图,正方体ABCD=A1B1C1D1,棱长为a,E、F分别为AB、BC上的点,且AE=BF=x.
如图,正方体ABCD=A1B1C1D1,棱长为a,E、F分别为AB、BC上的点,且AE=BF=x.