题目内容
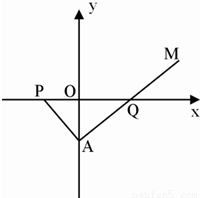
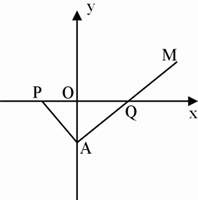
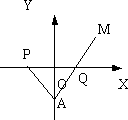
如图:在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°.在AQ的延长线上取一点M,使|AQ|=|MQ|(1)当点A在y轴上移动时,求动点M的轨迹E;(2)直线l:y=k(x+1)与轨迹E交于B、C两点.已知点F的坐标为(1,0),当∠BFC为锐角时,求k的取值范围.
答案:
解析:
解析:
|
(1)设动点M(x,y),过点M作 则 (2)假设直线 由方程组 直线L与抛物线交于不同两点B、C 由韦达定理得: 又 结合式子,从图形可知,当 |

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 消去y整理得:
消去y整理得:
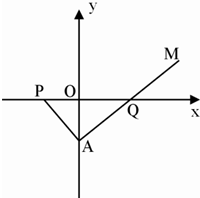 如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.
如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|. 如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.
如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.