题目内容
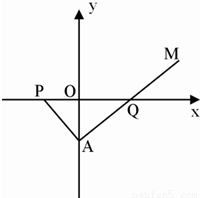
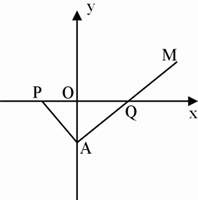
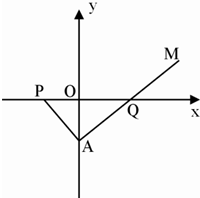 如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.
如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.(1)当点A在y轴上移动时,求动点M的轨迹E;
(2)直线l:y=kx-1与轨迹E交于B、C两点,已知点F的坐标为(1,0),当∠BFC为钝角时,求k的取值范围.
分析:(1)设A(0,b),Q(a,0),M(x,y)又M在AQ的延长线且|AQ|=|QM|,得到
=
,得到a,b与x,y的关系,
又△PAQ为直角三角形,得到b2=8a,将a,b用x,y代替即可.
(2)将直线方程与抛物线方程联立,利用韦达定理得到x1x2=
,x1+x2=
,将∠BFC为钝角转化为两向量的数量积小于0但不为-1,列出关于k的不等式,求出k的范围.
| AQ |
| QM |
又△PAQ为直角三角形,得到b2=8a,将a,b用x,y代替即可.
(2)将直线方程与抛物线方程联立,利用韦达定理得到x1x2=
| 1 |
| k2 |
| 2k+4 |
| k2 |
解答:解:(1)设A(0,b),Q(a,0),M(x,y)
Q在x轴正半轴上,∴a>0
又M在AQ的延长线且|AQ|=|QM|
∴
=
…(2分)
即(a,-b)=(x-a,y)
∴
…(4分)
又△PAQ为直角三角形
∴b2=8a
∴y2=4x(x>0)…(6分)
点M的轨迹E是焦点为(1,0),顶点在原点的抛物线不包括顶点(0,0)…(8分)
(2)设B(x1,y1),C(x2,y2)
由
得 k2x2-(2k+4)x+1=0
所以x1x2=
,x1+x2=
∵l与E有两个交点
∴
得k>-1且k≠0①…(8分)
∵∠BFC为钝角
∴
•
=(x1-1)(x2-1)+y1y2=(x1-1)(x2-1)+(kx1-1)(kx2-1)<0
即(k2+1)x1x2-(1+k)(x1+x2)+2<0
∴
-(1+k)
+2<0
得 k2-6k-3<0
解得 3-2
<k<3+2
②…(10分)
当
、
反向共线时,k=1 ③…(12分)
综合①②③得,k的取值范围:(3-2
,0)∪(0,1)∪(1,3+2
…(14分)
Q在x轴正半轴上,∴a>0
又M在AQ的延长线且|AQ|=|QM|
∴
| AQ |
| QM |
即(a,-b)=(x-a,y)
∴
|
又△PAQ为直角三角形
∴b2=8a
∴y2=4x(x>0)…(6分)
点M的轨迹E是焦点为(1,0),顶点在原点的抛物线不包括顶点(0,0)…(8分)
(2)设B(x1,y1),C(x2,y2)
由
|
所以x1x2=
| 1 |
| k2 |
| 2k+4 |
| k2 |
∵l与E有两个交点
∴
|
∵∠BFC为钝角
∴
| FB |
| FC |
即(k2+1)x1x2-(1+k)(x1+x2)+2<0
∴
| k2+1 |
| k2 |
| 2k+4 |
| k2 |
得 k2-6k-3<0
解得 3-2
| 3 |
| 3 |
当
| FB |
| FC |
综合①②③得,k的取值范围:(3-2
| 3 |
| 3) |
点评:解决直线与圆锥曲线的位置关系的问题,一般将直线方程与圆锥曲线方程联立,利用韦达定理,然后再找突破口.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
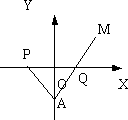
 如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.
如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.