题目内容
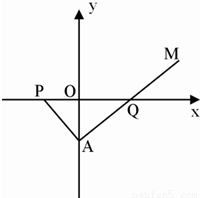
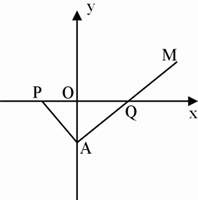
如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.
(1)当点A在y轴上移动时,求动点M的轨迹E;
(2)直线l:y=kx-1与轨迹E交于B、C两点,已知点F的坐标为(1,0),当∠BFC为钝角时,求k的取值范围.
【答案】
解:(1)设A(0,b),Q(a,0),M(x,y)
Q在x轴正半轴上,∴a>0
又M在AQ的延长线且|AQ|=|QM|
∴ …………………………………………………………2分
…………………………………………………………2分
即
∴ …………………………………………………………………4分
…………………………………………………………………4分
又△PAQ为直角三角形
∴b2=8a
∴ ……………………………………………………………6分
……………………………………………………………6分
点M的轨迹E是焦点为(1,0),顶点在原点的抛物线不包括顶点(0,0)……8分
(2)设
由 得
得 

∵l与E有两个交点
∴
 得
得 ① ………………………………………8分
① ………………………………………8分
∵∠BFC为钝角
∴
即
∴
得 
解得
 ②……………………………………………10分
②……………………………………………10分
当 、
、 反向共线时,k=1 ③…………………………………………………12分
反向共线时,k=1 ③…………………………………………………12分
综合①②③得,k的取值范围: …………………14分
…………………14分

练习册系列答案
相关题目
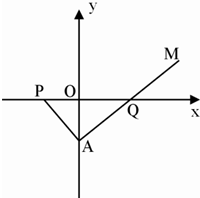 如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.
如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.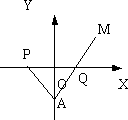
 如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.
如图,在Rt△PAQ中,点P的坐标为(-8,0),点A在y轴上,点Q在x轴的正半轴上,∠PAQ=90°,在AQ的延长线上取一点M,使|AQ|=|MQ|.