题目内容
在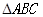 中,角
中,角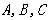 的对边分别为
的对边分别为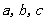 .且
.且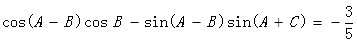
(1)求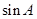 的值;
的值;
(2)若 ,求向量
,求向量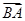 在
在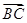 方向上的投影.
方向上的投影.
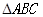 中,角
中,角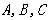 的对边分别为
的对边分别为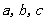 .且
.且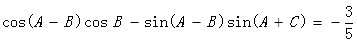
(1)求
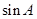 的值;
的值;(2)若
 ,求向量
,求向量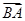 在
在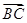 方向上的投影.
方向上的投影. (1)
(1)  (2)
(2)
试题分析:(1)此类问题需要进行两个统一:1、角的统一2、三角函数的统一,在三角函数的统一过程中往往应用三角的和差倍角公式,因此本题将角A+C转化为B,在应用两角和的余弦公式求出csoA=
 ,从而sinA=
,从而sinA= .
.(2)本题需要搞清投影的概念,向量
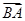 在向量
在向量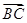 方向的投影为
方向的投影为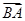 的模与两个向量夹角余弦的乘积,即
的模与两个向量夹角余弦的乘积,即 ,本类问题容易在向量的夹角上设计易错点,需要搞清夹角的概念.
,本类问题容易在向量的夹角上设计易错点,需要搞清夹角的概念.(1)
 由于
由于
所以

 ,
, .
.(2)由正弦定理可知
 ,由题意可知a>b则A>B,故A=
,由题意可知a>b则A>B,故A= ,由余弦定理可知
,由余弦定理可知 由余弦定理可知,解得c=1,或者c=-7(舍去).向量
由余弦定理可知,解得c=1,或者c=-7(舍去).向量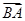 在向量
在向量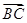 方向的投影
方向的投影 .
. .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的∠AOB的角平分线上的一点,且OM=1,过M任作一直线与∠AOB的两边分别交OA、OB于点E,F,记∠OEM=x.
的∠AOB的角平分线上的一点,且OM=1,过M任作一直线与∠AOB的两边分别交OA、OB于点E,F,记∠OEM=x.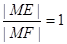 时,试问x的值为多少?(2)求
时,试问x的值为多少?(2)求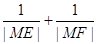 的取值范围.
的取值范围.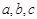 分别是
分别是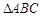 中角
中角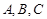 的对边,且
的对边,且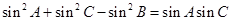 ,
,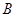 的大小;⑵若
的大小;⑵若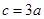 ,求
,求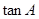 的值.
的值.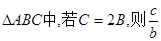 的范围是( )
的范围是( )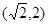
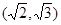

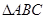 中,
中,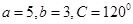 ,则
,则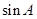 的值为( )
的值为( )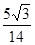
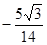
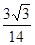
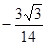
 的南偏西
的南偏西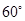 方向的
方向的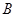 处,且与岛屿
处,且与岛屿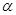 的方向追赶渔船乙,刚好用2小时追上.则
的方向追赶渔船乙,刚好用2小时追上.则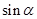 = .
= .
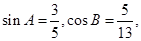 则
则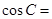 .
. 中,
中, 若三角形有两解,则
若三角形有两解,则 的取值范围是 .
的取值范围是 .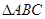 为锐角三角形,
为锐角三角形,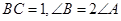 ,则
,则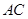 的取值范围为_______.
的取值范围为_______.