题目内容
11.设M,N是△ABC所在平面内不同的两点,且$\overrightarrow{AM}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),$\overrightarrow{AN}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$,则△ABM与△ABN的面积比$\frac{{S}_{△ABM}}{{S}_{△ABN}}$为( )| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{1}{3}$ |
分析 根据向量加法的平行四边形法则,过N作ND∥AC,交AB于D,则$DN=\frac{2}{3}AC$,从而可得到${S}_{△ABN}=\frac{2}{3}{S}_{△ABC}$,而由$\overrightarrow{AM}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$便知M为BC的中点,从而${S}_{△ABM}=\frac{1}{2}{S}_{△ABC}$,这样便可得出$\frac{{S}_{△ABM}}{{S}_{△ABN}}$的值.
解答 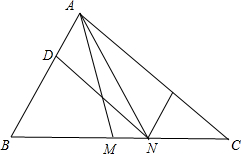 解:如图,过N作ND∥AC,交AB于D,$\overrightarrow{AN}=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$,∴$DN=\frac{2}{3}AC$;
解:如图,过N作ND∥AC,交AB于D,$\overrightarrow{AN}=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$,∴$DN=\frac{2}{3}AC$;
∴${S}_{△ABN}=\frac{2}{3}{S}_{△ABC}$;
$\overrightarrow{AM}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$;
∴M是BC中点;
∴${S}_{△ABM}=\frac{1}{2}{S}_{△ABC}$;
∴$\frac{{S}_{△ABM}}{{S}_{ABN}}=\frac{\frac{1}{2}}{\frac{2}{3}}=\frac{3}{4}$.
故选A.
点评 考查向量加法的平行四边形法则,向量数乘的几何意义,以及三角形的面积公式.

练习册系列答案
相关题目
1.定积分$\int_{-2π}^{2π}{({2x-sinx})}$的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
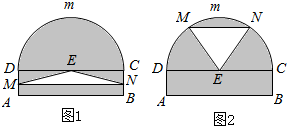 某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定