题目内容
已知A＝{x|ax－1>0}，B＝{x|x2－3x＋2>0}．
(1) 若A∩B＝A，求实数a的取值范围；
(2) 若A∩∁RB≠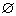
，求实数a的取值范围．
解：(1) 由于A∩B＝A 得A
B，由题意知B＝{x|x>2或x<1}．若a>0，则x>
≥2，得0＜a≤
；若a＝0，则A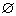＝，成立；若a＜0，则x＜＜1，根据数轴可知均成立．综上所述，a≤.
(2) ∁RB＝{x|1≤x≤2}，若a＝0，则A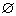＝，不成立；若a＜0，则x＜＜1，不成立；若a＞0，则x＞，由＜2得a＞.综上所述，a＞.
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
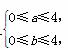x1，x2是关于x的方程x2－2x＋b－a＋3＝0的两个实根，则不等式0＜x1＜1＜x2成立的概率是( )
B.
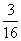
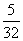D.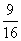
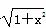)，是奇函数，p2：函数y＝x
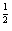为偶函数，则下列四个命题：
p1)∨p2；④ p1∧(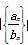
的前n项和Tn.