题目内容
设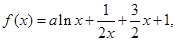 其中
其中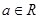 ,曲线
,曲线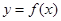 在点
在点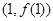 处的切线垂直于
处的切线垂直于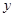 轴.
轴.
(Ⅰ) 求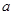 的值;
的值;
(Ⅱ) 求函数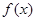 的极值.
的极值.
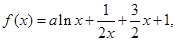 其中
其中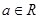 ,曲线
,曲线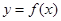 在点
在点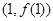 处的切线垂直于
处的切线垂直于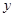 轴.
轴.(Ⅰ) 求
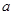 的值;
的值;(Ⅱ) 求函数
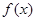 的极值.
的极值.(1) ;(2)
;(2) 在
在 处取得极小值
处取得极小值
 ;(2)
;(2) 在
在 处取得极小值
处取得极小值
试题分析:(1)因
 ,故
,故
由于曲线
 在点
在点 处的切线垂直于
处的切线垂直于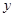 轴,故该切线斜率为0,即
轴,故该切线斜率为0,即 ,
,从而
 ,解得
,解得
(2)由(1)知
 ,
,

令
 ,解得
,解得 (因
(因 不在定义域内,舍去),
不在定义域内,舍去),当
 时,
时, ,故
,故 在
在 上为减函数;
上为减函数;当
 时,
时, ,故
,故 在
在 上为增函数;
上为增函数;故
 在
在 处取得极小值
处取得极小值
点评:典型题,本题属于导数应用中的基本问题,(2)通过研究导数的正负,明确了函数的单调性及极值情况。

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
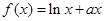 有小于1的极值点,则实数
有小于1的极值点,则实数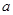 的取值范围是( )
的取值范围是( )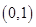
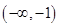
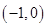
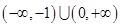
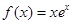 .
.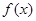 的单调区间与极值;
的单调区间与极值;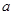 ,使得对任意的
,使得对任意的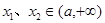 ,当
,当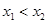 时恒有
时恒有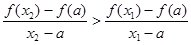 成立.若存在,求
成立.若存在,求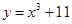 在点P(1,12)处的切线与两坐标轴围成三角形的面积是
在点P(1,12)处的切线与两坐标轴围成三角形的面积是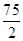
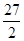
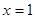 是函数
是函数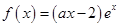 的一个极值点.
的一个极值点.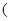
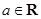
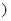
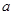 的值;
的值;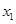 ,
,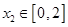 时,证明:
时,证明: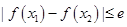
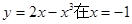 处的切线方程为( )
处的切线方程为( )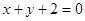
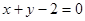
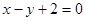
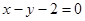
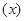 = f
= f
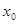 叫做函数的“新驻点”,若函数g
叫做函数的“新驻点”,若函数g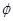
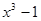 的“新驻点”分别为
的“新驻点”分别为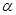 ,
,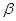 ,
,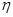 ,则的大小关系为 ( )
,则的大小关系为 ( )  在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间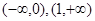 上是减函数,又
上是减函数,又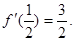
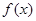 的解析式;
的解析式;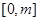 (m>0)上恒有
(m>0)上恒有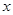 成立,求m的取值范围.
成立,求m的取值范围.