题目内容
(本题满分12分)已知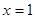 是函数
是函数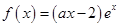 的一个极值点.
的一个极值点.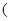
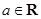
(Ⅰ)求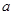 的值;
的值;
(Ⅱ)当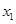 ,
,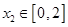 时,证明:
时,证明: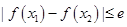
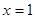 是函数
是函数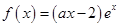 的一个极值点.
的一个极值点.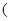
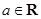
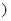
(Ⅰ)求
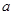 的值;
的值;(Ⅱ)当
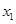 ,
,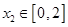 时,证明:
时,证明: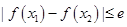
(1)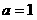 (2)要证明差的绝对值小于等于e,只要证明差介于-e和e之间即可,求解函数的 最值的差可知。
(2)要证明差的绝对值小于等于e,只要证明差介于-e和e之间即可,求解函数的 最值的差可知。
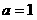 (2)要证明差的绝对值小于等于e,只要证明差介于-e和e之间即可,求解函数的 最值的差可知。
(2)要证明差的绝对值小于等于e,只要证明差介于-e和e之间即可,求解函数的 最值的差可知。试题分析:(Ⅰ)解:
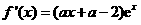 , 2分
, 2分由已知得
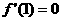 ,解得
,解得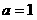 .
.当
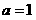 时,
时,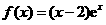 ,在
,在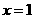 处取得极小值.
处取得极小值.所以
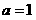 . 4分
. 4分(Ⅱ)证明:由(Ⅰ)知,
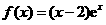 ,
,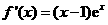 .
. 当
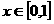 时,
时,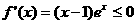 ,
,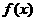 在区间
在区间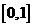 单调递减;
单调递减;当
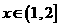 时,
时,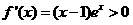 ,
,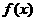 在区间
在区间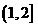 单调递增.
单调递增. 所以在区间
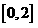 上,
上,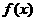 的最小值为
的最小值为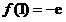 . 8分
. 8分又
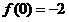 ,
,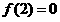 ,
,所以在区间
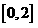 上,
上,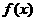 的最大值为
的最大值为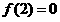 . 10分
. 10分 对于
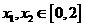 ,有
,有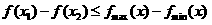 .
.所以
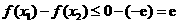 . 12分
. 12分点评:解决的关键是利用导数判定单调性,并能结合函数的最值来证明不等式,属于中档题。

练习册系列答案
相关题目
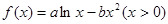 。(Ⅰ)若函数
。(Ⅰ)若函数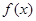 在
在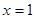 处与直线
处与直线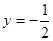 相切,①求实数
相切,①求实数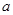 ,b的值;②求函数
,b的值;②求函数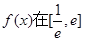 上的最大值;(Ⅱ)当
上的最大值;(Ⅱ)当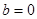 时,若不等式
时,若不等式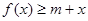 对所有的
对所有的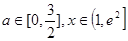 都成立,求实数m的取值范围。
都成立,求实数m的取值范围。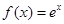 ,其图像在点
,其图像在点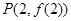 处的切线为
处的切线为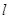 .
.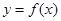 、直线
、直线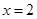 及两坐标轴围成的图形绕
及两坐标轴围成的图形绕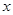 轴旋转一周所得几何体的体积;
轴旋转一周所得几何体的体积;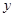 轴围成图形的面积.
轴围成图形的面积.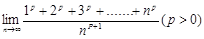 表示成定积分( )
表示成定积分( )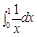
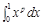
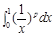
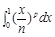
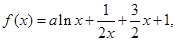 其中
其中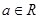 ,曲线
,曲线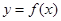 在点
在点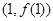 处的切线垂直于
处的切线垂直于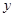 轴.
轴.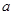 的值;
的值;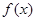 的极值.
的极值.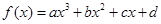 (
(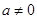 ),定义:设f″(x)是函数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数
),定义:设f″(x)是函数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数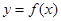 的“拐点”.有同学发现:“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,若函数
的“拐点”.有同学发现:“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,若函数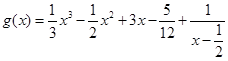 ,则
,则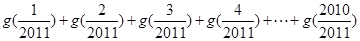 =( )
=( )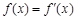 的函数是
的函数是 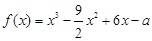 .
.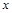 ,
,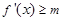 在
在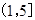 恒成立(其中
恒成立(其中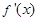 表示
表示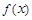 的导函数),求
的导函数),求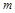 的最大值;
的最大值;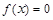 在
在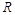 上有且仅有一个实根,求
上有且仅有一个实根,求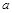 的取值范围.
的取值范围.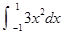 的值等于 .
的值等于 .