题目内容

函数y=
1-2sinx
的定义域是
[2kπ+
5
6
π，2kπ+
11
6
π]k∈Z
[2kπ+
5
6
π，2kπ+
11
6
π]k∈Z
．
分析：根据根号有意义的条件和三角函数的性质求出函数y的定义域；
解答：解：数y=
1-2sinx
，
∴1-2sinx≥0，可得
sinx≤
1
2
，正弦函数周期为2kπ，k∈Z，
解得
5π
6
+2kπ≤x≤
11π
6
+2kπ，k∈Z，
故答案为：[2kπ+
5
6
π，2kπ+
11
6
π]k∈Z；
点评：此题主要考查三角函数的性质，是一道基础题，注意三角函数的周期性；
练习册系列答案
相关题目
设函数y=1-2sin（
π
4
-x）cos（
π
4
-x），x∈R，则该函数是（　　）
下列命题中正确的是（　　）
（2012•三明模拟）（1）选修4-2：矩阵与变换
设矩阵M=
1a
b1
．
（I）若a=2，b=3，求矩阵M的逆矩阵M-1；
（II）若曲线C：x2+4xy+2y2=1在矩阵M的作用下变换成曲线C'：x2-2y2=1，求a+b的值．
（2）选修4-4：坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系中x轴的正半轴重合．圆C的参数方程为
x=1+2cosα
y=-1+2sinα
（α为参数），点Q极坐标为(2，
7π
4
)．
（Ⅰ）化圆C的参数方程为极坐标方程；
（Ⅱ）若点P是圆C上的任意一点，求P、Q两点距离的最小值．
（3）选修4-5：不等式选讲
设函数f（x）=|x+1|+|x-2|．
（Ⅰ）求y=f（x）的最小值；
（Ⅱ）若关于x的不等式f（x）≥4的解集为A，求集合A．
设函数y=1-2sin（-x）cos（-x），x∈R，则该函数是（ ）
A．最小正周期为的奇函数
B．最小正周期为的偶函数
C．最小正周期为π的奇函数
D．最小正周期为π的偶函数
设函数y=1-2sin（
π
4
-x）cos（
π
4
-x），x∈R，则该函数是（　　）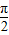
A．最小正周期为
π
2
的奇函数
B．最小正周期为
π
2
的偶函数
C．最小正周期为π的奇函数
D．最小正周期为π的偶函数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网