题目内容
(本小题满分12分)
已知数列 满足
满足 ,且
,且 (
( )。
)。
(1) 求 、
、 、
、 的值;
的值;
(2) 猜想数列 的通项公式,并用数学归纳法加以证明。
的通项公式,并用数学归纳法加以证明。
已知数列
 满足
满足 ,且
,且 (
( )。
)。(1) 求
 、
、 、
、 的值;
的值;(2) 猜想数列
 的通项公式,并用数学归纳法加以证明。
的通项公式,并用数学归纳法加以证明。(1) ,
, ,
,
(2) 有
有 成立。
成立。
 ,
, ,
,
(2)
 有
有 成立。
成立。解:(1)由题得 ,又
,又 ,
,
则 ,
, ,
, …………3分
…………3分
(2)猜想 。 …………………………………5分
。 …………………………………5分
证明:①当 时,
时, ,故命题成立。
,故命题成立。
②假设当 时命题成立,即
时命题成立,即 ………………………………7分
………………………………7分
则当 时,
时, ,
,
故命题也成立。 …………………………………11分
综上,对一切 有
有 成立。 …………………………………12分
成立。 …………………………………12分
 ,又
,又 ,
,则
 ,
, ,
, …………3分
…………3分(2)猜想
 。 …………………………………5分
。 …………………………………5分证明:①当
 时,
时, ,故命题成立。
,故命题成立。②假设当
 时命题成立,即
时命题成立,即 ………………………………7分
………………………………7分则当
 时,
时, ,
,故命题也成立。 …………………………………11分
综上,对一切
 有
有 成立。 …………………………………12分
成立。 …………………………………12分
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
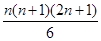
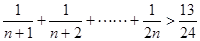 时,由k到k+1,不等式左端的变化是( )
时,由k到k+1,不等式左端的变化是( ) 项
项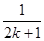 和
和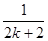 两项
两项 一项
一项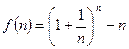 ,其中
,其中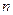 为正整数.
为正整数. ,
,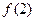 ,
,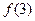 的值;
的值; 的正整数
的正整数 S2n<3,求q的取值范围
S2n<3,求q的取值范围 对一切正整数n都成立?证明你的结论
对一切正整数n都成立?证明你的结论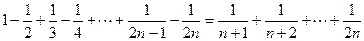
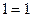 ,
,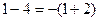 ,
,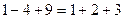 ,
,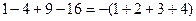 ,则第5个等式为 ,…,推广到第
,则第5个等式为 ,…,推广到第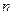 个等式为__ _;(注意:按规律写出等式的形式,不要求计算结果.)
个等式为__ _;(注意:按规律写出等式的形式,不要求计算结果.)