题目内容
设函数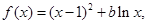 其中
其中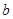 为常数.
为常数.
(Ⅰ)若函数 有极值点,求
有极值点,求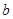 的取值范围及
的取值范围及 的极值点;
的极值点;
(Ⅱ)证明:对任意不小于3的正整数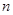 ,不等式
,不等式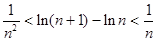 都成立.
都成立.
【答案】



【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
设函数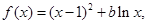 其中
其中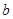 为常数.
为常数.
(Ⅰ)若函数 有极值点,求
有极值点,求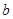 的取值范围及
的取值范围及 的极值点;
的极值点;
(Ⅱ)证明:对任意不小于3的正整数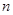 ,不等式
,不等式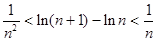 都成立.
都成立.



【解析】略

 阅读快车系列答案
阅读快车系列答案