题目内容
20.已知α是三角形的一个内角,且sinα•cosα=-$\frac{1}{8}$,则cosα-sinα=-$\frac{\sqrt{5}}{2}$.分析 由已知得sinα>0,cosα<0,(cosα-sinα)2=cos2α+sin2α-2sinαcosα=$\frac{5}{4}$,由此能求出cosα-sinα.
解答 解:∵α是三角形的一个内角,且sinα•cosα=-$\frac{1}{8}$,
∴sinα>0,cosα<0,
∴(cosα-sinα)2=cos2α+sin2α-2sinαcosα=1+$\frac{1}{4}$=$\frac{5}{4}$,
∴cosα-sinα=-$\sqrt{\frac{5}{4}}$=-$\frac{\sqrt{5}}{2}$.
故答案为:-$\frac{\sqrt{5}}{2}$.
点评 本题考查三个函数值的求法,是基础题,解题时要认真审题,注意同角三角函数关系式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知cos(α-β)=-$\frac{4}{5}$,sin(α+β)=-$\frac{3}{5}$,$\frac{π}{2}$<α-β<π,$\frac{3π}{2}$<α+β<2π,求β的值.
12.函数f(x)=x2对于任意的x,y∈R都有( )
| A. | f(x+y)=f(x)f(y) | B. | f(xy)=f(x)+f(y) | C. | f(xy)=f(x)f(y) | D. | f(x+y)=f(x)+f(y) |
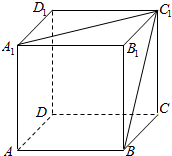 在正方体ABCD-A1B1C1D1中,求:
在正方体ABCD-A1B1C1D1中,求: 如图所示,已知在四棱锥P-ABCD中,CD∥AB,AD⊥AB,BC⊥PC,且AD=DC=PA=$\frac{1}{2}$AB=1
如图所示,已知在四棱锥P-ABCD中,CD∥AB,AD⊥AB,BC⊥PC,且AD=DC=PA=$\frac{1}{2}$AB=1 在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠BAD=60°,AE⊥BD.
在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠BAD=60°,AE⊥BD. 在长方体ABCD-A1B1C1D1中,AB=BC=1,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为$\frac{5}{3}$.则长方体外接球的表面积是6π.
在长方体ABCD-A1B1C1D1中,AB=BC=1,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为$\frac{5}{3}$.则长方体外接球的表面积是6π.