题目内容
已知△ABC三边之比为a:b:c=3:5:7,且最大边边长为14,则△ABC面积为
- A.15
- B.15

- C.15

- D.15

C
分析:先根据三边的比确定最大边,进而可得c,再根据他们的比分别求得a和b,根据余弦定理求得cosA的值,进而求得sinA的值,最后根据三角形的面积公式得到答案.
解答:∵a:b:c=3:5:7,
∴c为三角形的最大边,即c=14
∴b=10,a=6
∴cosA= =
=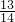
∴sinA=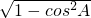 =
=
∴△ABC面积为 bcsinA=15
bcsinA=15
故选C.
点评:本题主要考查了余弦定理和三角形面积公式的应用.余弦定理、正弦定理和面积公式是解三角形问题的常用方法,故应熟练掌握.
分析:先根据三边的比确定最大边,进而可得c,再根据他们的比分别求得a和b,根据余弦定理求得cosA的值,进而求得sinA的值,最后根据三角形的面积公式得到答案.
解答:∵a:b:c=3:5:7,
∴c为三角形的最大边,即c=14
∴b=10,a=6
∴cosA=
 =
=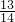
∴sinA=
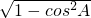 =
=
∴△ABC面积为
 bcsinA=15
bcsinA=15
故选C.
点评:本题主要考查了余弦定理和三角形面积公式的应用.余弦定理、正弦定理和面积公式是解三角形问题的常用方法,故应熟练掌握.

练习册系列答案
相关题目
已知△ABC三边之比为a:b:c=3:5:7,且最大边边长为14,则△ABC面积为( )
| A、15 | ||
B、15
| ||
C、15
| ||
D、15
|


