题目内容
若p：|3x-4|＞2；q：
＞0，则￢q是￢p的（ ）
| 1 |
| x2-x-2 |
分析：先求出p、q，进而求出￢p、￢q，利用充分必要条件的意义即可判断出结论．
解答：解：由|3x-4|＞2，∴3x-4＞2或3x-4＜-2，解得x＞2或x＜
．∴P：x＜
或x＞2．∴￢p：
≤x≤2．
由
＞0，得x2-x-2＞0，∴（x-2）（x+1）＞0，解得x＞2或x＜-1．∴q：x＞2或x＜-1，∴￢q：-1≤x≤2．
由上面可知：￢p⇒￢q，反之不成立．
故￢q是￢p的必要不充分条件．
故选C．
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
由
| 1 |
| x2-x-2 |
由上面可知：￢p⇒￢q，反之不成立．
故￢q是￢p的必要不充分条件．
故选C．
点评：正确理解充分必要条件和求出￢P与￢q是解题的关键．
练习册系列答案
相关题目
若p：|x+1|＞2和q：
＞0，则￢p是￢q（ ）条件．
| 1 |
| x2+3x-4 |
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
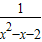＜0，则¬p是¬q的（ ）