题目内容
若p：|3x-4|＜2，q：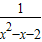
＜0，则¬p是¬q的（ ）A．充分而不必要条件
B．必要而不充分条件
C．充要条件
D．既不充分也不必要条件
【答案】分析：结合不等式的解法，利用充分条件和必要条件的定义进行判断．
解答：解：由|3x-4|＜2，得-2＜3x-4＜2，即
．
由
＜0得x2-x-2＜0，即-1＜x＜2．
所以q是p的必要不充分条件，
即¬p是¬q的必要不充分条件．
故选B．
点评：本题主要考查充分条件和必要条件的应用，利用逆否命题的等价性将￢p和¬q的关系转化为判断q是p的条件关系是解决本题的关键．
解答：解：由|3x-4|＜2，得-2＜3x-4＜2，即
．由
＜0得x2-x-2＜0，即-1＜x＜2．所以q是p的必要不充分条件，
即¬p是¬q的必要不充分条件．
故选B．
点评：本题主要考查充分条件和必要条件的应用，利用逆否命题的等价性将￢p和¬q的关系转化为判断q是p的条件关系是解决本题的关键．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
若p：|x+1|＞2和q：
＞0，则￢p是￢q（ ）条件．
| 1 |
| x2+3x-4 |
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |