题目内容
AB和平面M所成的角是a，AC在平面M内，AC和AB在平面M内的射影AB1所成的角是b，设∠BAC=q，求证：a、b、q满足关系式cosq=cosa·cosb
答案：
解析：
解析：
| 证明：如图，在B和AC确定的平面内作BD⊥AC，D为垂足，连结B1D．
∵BB1⊥平面M，AC ∴AC⊥平面BB1D，AC⊥B1D． 在Rt△ADB中，cosq=AD：AB， 在Rt△ABB1中，cosa=AB1：AB， 在Rt△ADB1中，cosb=AD：AB1， ∴cosa·cosb= 点评：由cosq=cosa·cosb，显然有cosq<cosa，由于a和q都是锐角，故a<q，即斜线和平面所成的角是斜线和平面内所有直线所成角中最小的角．
|
平面M，∴BB1⊥AC．
·
=
=cosq，
练习册系列答案
名校课堂系列答案
相关题目
（2010•衡阳模拟）如图，正方形ACDE所在的平面与平面ABC垂直，M是CE和AD的交点，AC⊥BC，且AC=BC．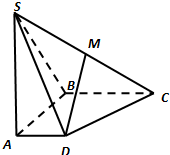
如图，在四棱锥S-ABCD中，底面ABCD是直角梯形，AD∥BC，SA⊥CD，AB⊥平面SAD，点M是SC的中点，且SA=AB=BC=1，AD=
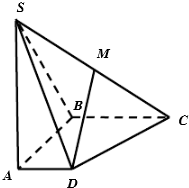如图，在四棱锥S-ABCD中，底面ABCD是直角梯形，AD∥BC，SA⊥CD，AB⊥平面SAD，点M是SC的中点，且SA=AB=BC=1，AD=