Question

【题目】为数列的前项和，已知，．

（1）求；

（2）记数列的前项和为，若对于任意的，恒成立，求实数的取值范围．

Answer 1

【答案】（1）（2）

【解析】

（1）由递推关系可得：（an+an﹣1）（an﹣an﹣1）＝2（an+an﹣1）．an＞0，可得an﹣an﹣1＝2（n≥2），利用等差数列的通项公式即可得出．

（2）利用“裂项求和”方法求Tn分离参数t，利用基本不等式求得最值即可得出．

（1）由，①

可知，②（n≥2）

①﹣②得：，

即（an+an﹣1）（an﹣an﹣1）＝2（an+an﹣1）．

∵an＞0，∴an+an﹣1≠0，

∴an﹣an﹣1＝2（n≥2），又

∴{an}是以a1＝3为首项，d＝2为公差的等差数列．

∴．

（2）．

Tn＝b1+b2+…+bn．

则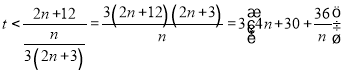

当且仅当取等，故