题目内容
已知各项为正数的数列{an}的前n项和为Sn,满足Sn+1=(Ⅰ)求an;
(Ⅱ)求bn;
(Ⅲ)令cn=![]() ,数列{cn}的前n项和为Tn,求证:Tn<3.
,数列{cn}的前n项和为Tn,求证:Tn<3.
解:(Ⅰ)令n=1,a1+1=![]() ,
,
∵a1+1>0,∴1=![]() ,a1=2
,a1=2
由已知得2Sn+2=![]() +an①
+an①
2Sn+1+2=![]() +an+1②
+an+1②
②-①得(an+1+an=![]() -
-![]() ,∵an>0,∴an+1-an=1
,∵an>0,∴an+1-an=1
∴数列{an}是以2为首项,以1为公差的等差数列,
∴an=n+1
(Ⅱ)由bn+2+2bn=3bn+1得bn+2-bn+1=2(bn+1-bn)
∵b1=2,b2=4,b2- b1=2,∴![]() =2
=2
∴数列{bn+1-bn}是以2为首项,以2为公比的等比数列
bn+1-bn=2n
b2-b1=2
b3-b2=22
b4-b3=23
……
bn-bn-1=2n-1
累加得bn=2n
(Ⅲ)cn=![]() =(n+1)
=(n+1)![]()
Tn=2×![]() +3(
+3(![]() )2+4(
)2+4(![]() )3+…+(n+1)(
)3+…+(n+1)(![]() )n③
)n③
![]() Tn=2(
Tn=2(![]() )2+3(
)2+3(![]() )3+…+n(
)3+…+n(![]() )n+(n+1)(
)n+(n+1)(![]() )n+1④
)n+1④
③-④并整理得Tn=3-![]() <3
<3

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
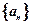 的前
的前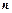 项和为
项和为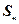 ,且满足
,且满足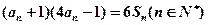 ,
,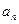
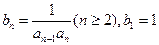 ,数列
,数列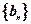 的前
的前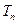 ,若
,若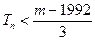 对一切
对一切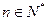 恒成立,求
恒成立,求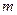 的最小值.
的最小值.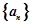 的前
的前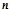 项和为
项和为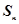 ,且满足
,且满足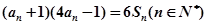 ,
,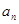
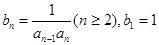 ,数列
,数列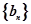 的前
的前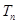 ,若
,若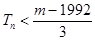 对一切
对一切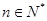 恒成立,求
恒成立,求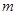 的最小值.
的最小值.