题目内容
已知各项为正数的数列{an}的前n项和为{Sn},首项为a1,且2,an,Sn成等差数列,
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=log2an,cn=
,求数列{cn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=log2an,cn=
| bn | an |
分析:(I)由题意可得,2an=2+Sn,结合2an-1=2+Sn-1(n≥2)可得数列an与an-1的关系,结合特殊数列的通项公式可求
(II)由bn=log2an=n,可得Cn=
=
,利用乘公比错位相减可求和
(II)由bn=log2an=n,可得Cn=
| bn |
| an |
| n |
| 2n |
解答:解:(I)由题意可得,2an=2+Sn①
∴2an-1=2+Sn-1(n≥2)②
①-②可得,an=2an-1(n≥2)
∵2a1=2+S1∴a1=2
由等比数列的通项公式可得,an=2n
(II)∵bn=log2an=n,Cn=
=
∴Tn=
+
+
+…+
①
∴
Tn=
+
+…+
+
②
①-②可得,
Tn=
+
+…+
-
=
-
∴Tn=2-
∴2an-1=2+Sn-1(n≥2)②
①-②可得,an=2an-1(n≥2)
∵2a1=2+S1∴a1=2
由等比数列的通项公式可得,an=2n
(II)∵bn=log2an=n,Cn=
| bn |
| an |
| n |
| 2n |
∴Tn=
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
∴
| 1 |
| 2 |
| 1 |
| 22 |
| 2 |
| 23 |
| n-1 |
| 2n |
| n |
| 2n+1 |
①-②可得,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| n |
| 2n+1 |
| ||||
1-
|
| n |
| 2n+1 |
∴Tn=2-
| 2+n |
| 2n |
点评:本题主要考查了利用数列的递推公式求解数列的通项公式,乘公比错位相减求解数列的和方法是数列求和的重点与难点.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
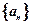 的前
的前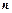 项和为
项和为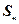 ,且满足
,且满足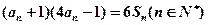 ,
,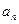
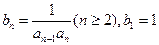 ,数列
,数列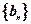 的前
的前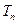 ,若
,若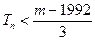 对一切
对一切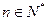 恒成立,求
恒成立,求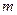 的最小值.
的最小值.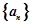 的前
的前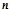 项和为
项和为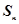 ,且满足
,且满足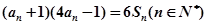 ,
,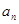
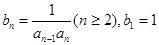 ,数列
,数列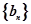 的前
的前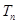 ,若
,若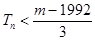 对一切
对一切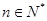 恒成立,求
恒成立,求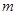 的最小值.
的最小值.