题目内容
14. 在多面体ABCDEFG中,四边形ABCD与ADEF是边长均为a的正方形,四边形ABGF是直角梯形,AB⊥AF,且FA=2FG=4FH.
在多面体ABCDEFG中,四边形ABCD与ADEF是边长均为a的正方形,四边形ABGF是直角梯形,AB⊥AF,且FA=2FG=4FH.(1)求证:平面BCG⊥平面EHG;
(2)若a=4,求四棱锥G-BCEF的体积.
分析 (1)连结BH,推导出HG⊥GB,DA⊥AF,DA⊥AB,CB⊥HG,从而HG⊥平面BCG,由此能证明平面BCG⊥平面EHG.
(2)过B作AF的平行线交FG的延长线于点P,连结AP、FB,交于点O,过G作GK⊥FB于K,由此能求出四棱锥G-BCEF的体积.
解答 证明:(1)连结BH,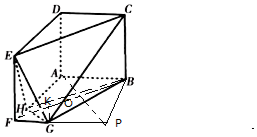
∵四边形ABCD与ADEF是边长均为a的正方形,四边形ABGF是直角梯形,AB⊥AF,且FA=2FG=4FH,
∴AH=$\frac{3}{4}a,AB=a$,∴HB=$\sqrt{(\frac{3}{4}a)^{2}+{a}^{2}}$=$\frac{5}{4}a$,HG=$\sqrt{(\frac{1}{4}a)^{2}+(\frac{1}{2}a)^{2}}$=$\frac{\sqrt{5}}{4}a$,
GB=$\sqrt{{a}^{2}+(\frac{1}{2}a)^{2}}$=$\frac{\sqrt{5}}{2}$a,
∴HB2=HG2+GB2,∴HG⊥GB,
∵DA⊥AF,DA⊥AB,∴DA⊥平面ABGH,
又∵CB∥DA,∴CB⊥平面ABGF,∴CB⊥HG,
∵GB∩CB=B,∴HG⊥平面BCG,
∵HG⊥平面EHG,∴平面BCG⊥平面EHG.
解:(2)过B作AF的平行线交FG的延长线于点P,连结AP、FB,交于点O,
过G作GK⊥FB于K,则GK=$\frac{1}{2}PD=\frac{1}{2}×2\sqrt{2}=\sqrt{2}$,
∴四边形BCEF的面积S=4×$4\sqrt{2}$=16$\sqrt{2}$,
∴四棱锥G-BCEF的体积VG-BCEF=$\frac{1}{3}×16\sqrt{2}×\sqrt{2}$=$\frac{32}{3}$.
点评 本题考查面面垂直的证明,考查四棱锥的体积,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

| A. | $\frac{4}{5}$ | B. | 1 | C. | $\frac{8}{5}$ | D. | 2 |
| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | $\sqrt{3}$ |
 如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,M,N分别为B1C,A1A上的点,且$\frac{{B}_{1}M}{MC}$=$\frac{{A}_{1}N}{NA}$=$\frac{1}{3}$
如图,在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,M,N分别为B1C,A1A上的点,且$\frac{{B}_{1}M}{MC}$=$\frac{{A}_{1}N}{NA}$=$\frac{1}{3}$ 执行如图的程序框图,则输出的i=6.([$\frac{S}{3}$]表示不超过$\frac{S}{3}$的最大整数)
执行如图的程序框图,则输出的i=6.([$\frac{S}{3}$]表示不超过$\frac{S}{3}$的最大整数)