题目内容
PQ过△OAB的重心G, ,则
,则 =
=
- A.3
- B.

- C.2
- D.1
A
分析:由三角形的重心的性质可得,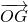 =
= =
= =
= ,根据
,根据 ∥
∥ ,可得(
,可得(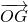 -
- )=λ (
)=λ (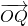 -
-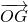 ),化简可得3mn=m+n,即
),化简可得3mn=m+n,即 =3.
=3.
解答:设AB的中点为E,由三角形的重心的性质可得,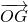 =
= =
= =
= .
.
又PQ过△OAB的重心G,∴ ∥
∥ ,∴(
,∴(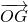 -
- )=λ (
)=λ (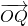 -
-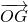 ),
),
(1-3m) +
+ =λ[-
=λ[- +(3n-1)
+(3n-1) ],∴1-3m=-λ,1=λ (3n-1),
],∴1-3m=-λ,1=λ (3n-1),
化简可得3mn=m+n,∴ =3,
=3,
故选A.
点评:本题考查本题考查两个向量的加减法的法则以及其几何意义,根据题意得到(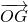 -
- )=λ (
)=λ (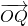 -
-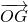 ),是解题的关键.
),是解题的关键.
分析:由三角形的重心的性质可得,
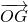 =
= =
= =
= ,根据
,根据 ∥
∥ ,可得(
,可得(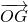 -
- )=λ (
)=λ (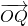 -
-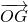 ),化简可得3mn=m+n,即
),化简可得3mn=m+n,即 =3.
=3.解答:设AB的中点为E,由三角形的重心的性质可得,
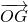 =
= =
= =
= .
.又PQ过△OAB的重心G,∴
 ∥
∥ ,∴(
,∴(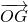 -
- )=λ (
)=λ (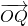 -
-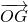 ),
),(1-3m)
 +
+ =λ[-
=λ[- +(3n-1)
+(3n-1) ],∴1-3m=-λ,1=λ (3n-1),
],∴1-3m=-λ,1=λ (3n-1),化简可得3mn=m+n,∴
 =3,
=3,故选A.
点评:本题考查本题考查两个向量的加减法的法则以及其几何意义,根据题意得到(
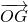 -
- )=λ (
)=λ (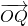 -
-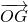 ),是解题的关键.
),是解题的关键. 
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
PQ过△OAB的重心G,
=
,
=
,
=m
,
=n
,则
+
=( )
| OA |
| a |
| OB |
| b |
| OP |
| a |
| OQ |
| b |
| 1 |
| m |
| 1 |
| n |
| A、3 | ||
B、
| ||
| C、2 | ||
| D、1 |
 如图,PQ过△OAB的重心G,设
如图,PQ过△OAB的重心G,设 =
= ,
, =
= ;若
;若 =m
=m ,
, =n
=n ,则
,则 +
+ = .
= .