题目内容
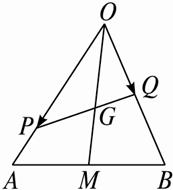
如图，PQ过△OAB的重心G，设| OA |
| a |
| OB |
| b |
| OP |
| a |
| OQ |
| b |
| 1 |
| m |
| 1 |
| n |
分析：根据PQ过△OAB的重心G，而本题对于PQ没有特别的限制，做这种填空题目可以使得PQ平行于AB，当这两条线是一个平行关系时，根据重心的性质得到共线的两个向量的模长之间的关系，得到m，n的值，得到结果．
解答：解：PQ过△OAB的重心G，对于PQ没有特别的限制，
∴可以使得PQ平行于AB，
当这两条线是一个平行关系时，
根据重心的性质，有
=
，
=
∴
+
=
+
=3
故答案为：3
∴可以使得PQ平行于AB，
当这两条线是一个平行关系时，
根据重心的性质，有
| OP |
| 2 |
| 3 |
| a |
| OQ |
| 2 |
| 3 |
| b |
∴
| 1 |
| m |
| 1 |
| n |
| 3 |
| 2 |
| 3 |
| 2 |
故答案为：3
点评：本题考查三角形的重心的性质，考查选择和填空的特殊的做法，即采用特殊值法，这样解题过程要简单得多，本题是一个基础题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
=a，
=b，
=ma，
=nb，求证：
=3.
=
，
=
；若
=m
，
=n
，则
+
= ．
=
，
=
；若
=m
，
=n
，则
+
= ．