题目内容
6. 如图,在直三角形ABC-A1B1C1中,M为AB1的中点,△CMB1为等边三角形
如图,在直三角形ABC-A1B1C1中,M为AB1的中点,△CMB1为等边三角形(1)证明:AC⊥平面BCC1B1
(2)设二面角B-CA-M的大小为60°,AB1=8,求点C1到平面CMB1的距离.
分析 (1)通过直三棱柱ABC-A1B1C1的性质知AC⊥C1C,利用线面垂直的判定定理即可;
(2)通过题意易得二面角B-CA-M的平面角为∠BCB1,过C1作C1N⊥CB1交CB1于N,则C1N即为点C1到平面CMB1的距离,在Rt△CB1C1中利用面积的不同计算方法计算即可.
解答 (1)证明:由直三棱柱ABC-A1B1C1的性质知AC⊥C1C,
∵M为AB1的中点,△CMB1为等边三角形,
∴MA=MB1=MC,∴AC⊥CB1,
又∵B1C∩C1C=C,
∴AC⊥平面BCC1B1;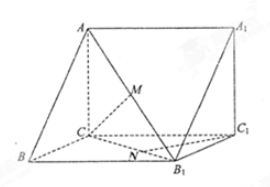 (2)解:由(1)知AC⊥平面BB1C1C,
(2)解:由(1)知AC⊥平面BB1C1C,
∴BC⊥AC,BC1⊥AC,
∴二面角B-CA-M的平面角为∠BCB1,即∠BCB1=60°,
在Rt△ACB1中,∵AB1=8,∴CM=CB1=4,
又∵∠BCB1=60°,∴BC=2,BB1=$2\sqrt{3}$,
过C1作C1N⊥CB1交CB1于N,
∵AC⊥平面BB1C1C,且C1N⊥CB1,
∴C1N即为点C1到平面CMB1的距离,
在Rt△CB1C1中,CC1•C1B1=B1C•C1N,
∴C1N=$\frac{C{C}_{1}•{C}_{1}{B}_{1}}{{B}_{1}C}$=$\frac{2\sqrt{3}×2}{4}$=$\sqrt{3}$.
点评 本题考查二面角,空间中线面的位置关系、点到面的距离,三角形的面积计算公式,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
17.已知函数f(x)是定义在R上周期为3的周期函数,当x∈[0,3)时,$f(x)=|{x^2}-2x+\frac{1}{2}|$,则函数f(x)在[-3,4]上的零点的个数为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
18.某程序框如所示,该程序运行后输出的S的值是( )


| A. | $\frac{1}{3}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
15.执行如图所示的程序框图,则输出结果为( )


| A. | 15 | B. | 16 | C. | 25 | D. | 36 |
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°PA=PD=AD=2BC=2,$CD=\sqrt{3},PB=\sqrt{6}$,Q是AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°PA=PD=AD=2BC=2,$CD=\sqrt{3},PB=\sqrt{6}$,Q是AD的中点. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC=4,E、F分别是PC、PD的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC=4,E、F分别是PC、PD的中点.