题目内容
已知数列{an}是首项为-1,公差d 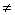 0的等差数列,且它的第2、3、6项依次构成等比数列{ bn}的前3项。
0的等差数列,且它的第2、3、6项依次构成等比数列{ bn}的前3项。
(1)求{an}的通项公式;(2)若Cn=an·bn,求数列{Cn}的前n项和Sn。
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
题目内容
已知数列{an}是首项为-1,公差d 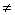 0的等差数列,且它的第2、3、6项依次构成等比数列{ bn}的前3项。
0的等差数列,且它的第2、3、6项依次构成等比数列{ bn}的前3项。
(1)求{an}的通项公式;(2)若Cn=an·bn,求数列{Cn}的前n项和Sn。
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案