题目内容
如图给出的是计算了| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 30 |
（ ）
分析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出S的值．
解答：解：程序运行过程中，各变量值如下表所示：
第一次循环：S=0+
，i=2，
第二次循环：S=
+
，i=3，
第三次循环：S=
+
+
，i=4，…
依此类推，第15次循环：
S=
+
+
+…+
，i=16，
退出循环
其中判断框内应填入的条件是：i＞15？
故答案为：B．
第一次循环：S=0+
| 1 |
| 2 |
第二次循环：S=
| 1 |
| 2 |
| 1 |
| 4 |
第三次循环：S=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
依此类推，第15次循环：
S=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 30 |
退出循环
其中判断框内应填入的条件是：i＞15？
故答案为：B．
点评：算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．程序填空也是重要的考试题型，这种题考试的重点有：①分支的条件②循环的条件③变量的赋值④变量的输出．其中前两点考试的概率更大．此种题型的易忽略点是：不能准确理解流程图的含义而导致错误．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16、给出50个数，1，3，7，13，21，…，其规律是：第1个数是1，第2个数比第1个数大2，第3个数比第2个数大4，第4个数比第3个数大6，…，以此类推．如图流程图给出了计算这50个数的和的一种算法，那么在（1）处应该填写的内容是
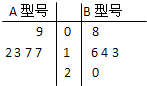某工厂生产A、B两种型号的产品，每种型号的产品在出厂时按质量分为一等品和二等品．为便于掌握生产状况，质检时将产品分为每20件一组，分别记录每组一等品的件数．现随机抽取了5组的质检记录，其一等品数茎叶图如图所示：（1）试根据茎叶图所提供的数据，分别计算A、B两种产品为一等品的概率PA、PB；
（2）已知每件产品的利润如表一所示，用ξ、η分别表示一件A、B型产品的利润，在（1）的条件下，求ξ、η的分布列及数学期望（均值）Eξ、Eη；
（3）已知生产一件产品所需用的配件数和成本资金如表二所示，该厂有配件30件，可用资金40万元，设x、y分别表示生产A、B两种产品的数量，在（2）的条件下，求x、y为何值时，z=xEξ+yEη最大？最大值是多少？（解答时须给出图示）
表一
| 等级 利润 产品 |
一等品 | 二等品 |
| A型 | 4（万元） | 3（万元） |
| B型 | 3（万元） | 2（万元） |
| 项目 用量 产品 |
配件（件） | 资金（万元） |
| A型 | 6 | 4 |
| B型 | 2 | 8 |
已知某人工养殖观赏鱼池塘中养殖着大量的红鲫鱼与中国金鱼．为了估计池塘中这两种鱼的数量，养殖人员从水库中捕出了红鲫鱼与中国金鱼各1000只，给每只鱼作上不影响其存活的记号，然后放回池塘，经过一定时间，再每次从池塘中随机地捕出1000只鱼，分类记录下其中有记号的鱼的数目，随即将它们放回池塘中．这样的记录作了10次，将记录获取的数据作成如图的茎叶图．
某工厂为了制造一个实心工件，先画出了这个工件的三视图（如图），其中正视图与侧视图为两个全等的等腰三角形，俯视图为一个圆，三视图尺寸如图所示（单位cm）；