题目内容
(本小题13分)已知函数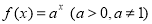 在区间[-1,2]上的最大值是最小值的8倍.
在区间[-1,2]上的最大值是最小值的8倍.
(Ⅰ)求a的值;
(Ⅱ)当a>1时,解不等式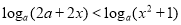 .
.
(1) 或
或 ;(2)
;(2) ;
;
【解析】
试题分析:(1)本题为指数函数类型,当底数 ,函数为减函数,当底数
,函数为减函数,当底数 ,函数为增函数,因此本题要注意分情况讨论;(2)当底数a>1时,对数函数为单调递增的,因此有
,函数为增函数,因此本题要注意分情况讨论;(2)当底数a>1时,对数函数为单调递增的,因此有 ,又因为对数函数中,真数需大于0,因此有
,又因为对数函数中,真数需大于0,因此有 ,综上所述,
,综上所述, ;
;
试题解析:(Ⅰ)当 时,
时, ,则
,则 ,解得
,解得 ;
;
当 时,
时, ,则
,则 ,解得
,解得 ;
;
综上: 或
或 ;
;
(Ⅱ)当 时,由前知
时,由前知 ,不等式
,不等式 ,即为
,即为 ,
,


得解集为. ;
;
考点:①指数函数的单调性②对数函数单调性的应用
考点分析: 考点1:不等式 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 为圆
为圆 的切线,
的切线, 为切点,
为切点,
 ,
,
 的角平分线与
的角平分线与 和圆
和圆 和
和 .
.

 的值.
的值. 若
若 与
与 平行,则实数
平行,则实数 的值是
的值是 是不等式组
是不等式组 表示的平面区域内的任意一点,向量
表示的平面区域内的任意一点,向量 ,
, ,若
,若 (
( 为实数),则
为实数),则 的最大值为
的最大值为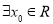 ,使得
,使得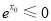
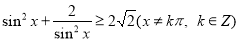

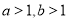 是
是 的充分不必要条件
的充分不必要条件 。
。 的部分图象如图所示,则
的部分图象如图所示,则 的解析式是( )
的解析式是( )
 B.
B.
 D.
D.
 =10,则
=10,则 等于( )
等于( )
 是等比数列,命题
是等比数列,命题 “若公比
“若公比 ,则数列
,则数列