题目内容
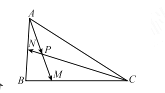
【题目】在 ![]() 中,
中, ![]() .
.
(1)求 ![]() 与
与 ![]() 的面积之比;
的面积之比;
(2)若 ![]() 为
为 ![]() 中点,
中点, ![]() 与
与 ![]() 交于点
交于点 ![]() ,且
,且 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:在 ![]() 中,
中, ![]() ,可得
,可得 ![]() ,即点
,即点 ![]() 在线段
在线段 ![]() 靠近
靠近 ![]() 点的四等分点. 故
点的四等分点. 故 ![]() 与
与 ![]() 的面积之比为
的面积之比为 ![]()
(2)解:因为 ![]() ,
,
![]() ,所以
,所以 ![]() ,
,
因为 ![]() 为
为 ![]() 中点,所以
中点,所以 ![]() ,
,
![]()
因为 ![]() ,所以
,所以 ![]() ,即
,即 ![]() ,
,
又 ![]() ,所以
,所以 ![]() ,所以
,所以 ![]() .
.
【解析】(1)由已知利用向量的线性运算得出向量共线,根据比值的关系可得出点 M 在线段 B C 靠近 B 点的四等分点,利用面积公式推导出 Δ A B M 与 Δ A B C 的面积之比为边之比为![]() 。(2)根据向量的线性运算可得出
。(2)根据向量的线性运算可得出![]() 和
和![]() 共线利用已知求出x = 3 y,再利用中点的性质结合向量的线性运算可得证
共线利用已知求出x = 3 y,再利用中点的性质结合向量的线性运算可得证![]() 和
和![]() 共线又得到2 x + y = 1,联立两式分别求出x、y的值即得结果。
共线又得到2 x + y = 1,联立两式分别求出x、y的值即得结果。

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目