题目内容
如图，在四棱锥
中，底面ABCD是正方形，侧棱
底面ABCD，
，
是PC的中点
（1）证明:
平面EDB；
（2）求EB与底面ABCD所成的角的正切值
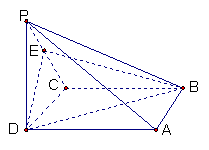
（1）证明：连结AC、AC交BD于O连结EO
∵ 底面ABCD是正方形 ∴ 点O是AC的中点
在
中，EO是中位线 ∴ 
而
平面EDB且
平面
，所以，平面EDB
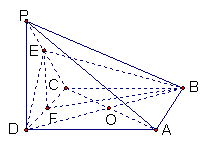
（2）解：作
交CD于F连结BF，设正方形ABCD的边长为
∵ 底面ABCD ∴ 
∴ 
F为DC的中点
∴ 
底面ABCD，BF为BE在底面ABCD内的射影，故
为直线EB与底面ABCD所成的角
在
中，
∵ 
∴ 在
中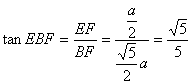 
所以EB与底面ABCD所成的角的正切值为
练习册系列答案
名校课堂系列答案
相关题目
中，底面
是矩形．已知
．
平面
；
与
所成的角的大小；
的大小．
中，底面
是菱形，
，
，
,
平面
是
的中点，
是
的中点. 
∥平面
；
；
所成的锐二面角的大小.
中，底面
是矩形．已知
．
平面
；
与
所成的角的大小；
的大小．
中，底面
是正方形，侧棱
，
为
中点，作
交
于
与平面
所成的锐二面角的正弦值。
中，底面
为平行四边形，
平面
在棱
上．
时，求证
平面
的大小为
时，求直线
与平面
所成角的正弦值．