题目内容
(2006•安徽)函数f(x)对于任意实数x满足条件f(x+2)=
,若f(1)=-5,则f[f(5)]=
| 1 |
| f(x) |
-
| 1 |
| 5 |
-
.| 1 |
| 5 |
分析:由已知中函数f(x)对于任意实数x满足条件f(x+2)=
,我们可确定函数f(x)是以4为周期的周期函数,进而根据周期函数的性质,从内到外依次去掉括号,即可得到答案.
| 1 |
| f(x) |
解答:解:∵函数f(x)对于任意实数x满足条件f(x+2)=
,
∴f(x+4)=f[(x+2)+2]=
=
=f(x),
即函数f(x)是以4为周期的周期函数,
∵f(1)=-5
∴f[f(5)]=f[f(1)]=f(-5)=f(3)=
=-
故答案为:-
| 1 |
| f(x) |
∴f(x+4)=f[(x+2)+2]=
| 1 |
| f(x+2) |
| 1 | ||
|
即函数f(x)是以4为周期的周期函数,
∵f(1)=-5
∴f[f(5)]=f[f(1)]=f(-5)=f(3)=
| 1 |
| f(1) |
| 1 |
| 5 |
故答案为:-
| 1 |
| 5 |
点评:本题考查的知识点是函数的周期性,函数的值,其中根据已知中函数f(x)对于任意实数x满足条件f(x+2)=
,判断出函数f(x)是以4为周期的周期函数,是解答本题的关键.
| 1 |
| f(x) |

练习册系列答案
相关题目
(2006
重庆模拟)函数f(x)和g(x)的定义域都是R,且f(x)≥0的解集为(1,2),g(x)≥0的解集为空集.则 的解集是
的解集是
[
]|
A .(1,2) |
B .(-∞,1]∪[2,+∞) |
|
C .(-1,1)∪[2,+∞) |
D .[1,2] |
(2006
黄冈模拟)函数f(x)的部分图象如图所示,则f(x)可以是[
]
|
A . |
B .2sinx+2 |
|
C . |
D . |
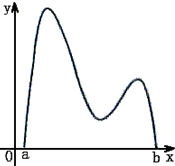 (2013•安徽)函数y=f(x)的图象如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2,…xn,使得
(2013•安徽)函数y=f(x)的图象如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2,…xn,使得