题目内容
(1)已知 =(2x-y+1,x+y-2),
=(2x-y+1,x+y-2), =(2,-2),①当x、y为何值时,
=(2,-2),①当x、y为何值时, 与
与 共线?②是否存在实数x、y,使得
共线?②是否存在实数x、y,使得 ⊥
⊥ ,且|
,且| |=|
|=| |?若存在,求出xy的值;若不存在,说明理由.
|?若存在,求出xy的值;若不存在,说明理由.(2)设
 和
和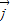 是两个单位向量,其夹角是90°,
是两个单位向量,其夹角是90°, ,若
,若 ,求实数k的值.
,求实数k的值.
【答案】分析:(1)①由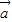 与
与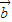 共线,可得存在非零实数λ使得
共线,可得存在非零实数λ使得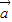 =λ
=λ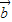 ,从而可得结论;
,从而可得结论;
②由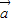 ⊥
⊥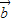 得,(2x-y+1)×2+(x+y-2)×(-2)=0,由|
得,(2x-y+1)×2+(x+y-2)×(-2)=0,由|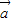 |=|
|=|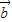 |得,(2x-y+1)2+(x+y-2)2=8,从而可得结论;
|得,(2x-y+1)2+(x+y-2)2=8,从而可得结论;
(2)利用向量的数量积公式,即可求实数k的值.
解答:解:(1)①∵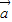 与
与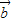 共线,
共线,
∴存在非零实数λ使得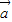 =λ
=λ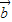 ,
,
∴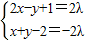
∴x= ,y∈R;
,y∈R;
②由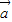 ⊥
⊥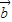 得,(2x-y+1)×2+(x+y-2)×(-2)=0
得,(2x-y+1)×2+(x+y-2)×(-2)=0
所以x-2y+3=0.(i)
由|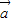 |=|
|=|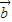 |得,(2x-y+1)2+(x+y-2)2=8.(ii)
|得,(2x-y+1)2+(x+y-2)2=8.(ii)
解(i)(ii)得 或
或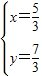 ;
;
(2)由题意,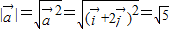 ,①
,①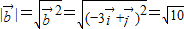 ,②
,②
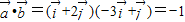 ③…(10分)
③…(10分)
∵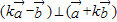 ,
,
∴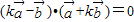 ,得,
,得,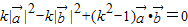
将①②③代入得:k2+5k-1=0,…(12分)
解得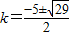 …(14分)
…(14分)
点评:本题考查向量共线、垂直的条件的运用,考查数量积公式,考查学生的计算能力,属于中档题.
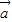 与
与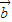 共线,可得存在非零实数λ使得
共线,可得存在非零实数λ使得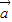 =λ
=λ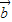 ,从而可得结论;
,从而可得结论;②由
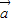 ⊥
⊥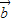 得,(2x-y+1)×2+(x+y-2)×(-2)=0,由|
得,(2x-y+1)×2+(x+y-2)×(-2)=0,由|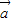 |=|
|=|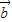 |得,(2x-y+1)2+(x+y-2)2=8,从而可得结论;
|得,(2x-y+1)2+(x+y-2)2=8,从而可得结论;(2)利用向量的数量积公式,即可求实数k的值.
解答:解:(1)①∵
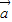 与
与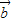 共线,
共线,∴存在非零实数λ使得
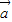 =λ
=λ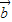 ,
,∴
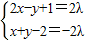
∴x=
 ,y∈R;
,y∈R;②由
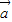 ⊥
⊥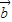 得,(2x-y+1)×2+(x+y-2)×(-2)=0
得,(2x-y+1)×2+(x+y-2)×(-2)=0所以x-2y+3=0.(i)
由|
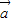 |=|
|=|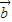 |得,(2x-y+1)2+(x+y-2)2=8.(ii)
|得,(2x-y+1)2+(x+y-2)2=8.(ii)解(i)(ii)得
 或
或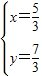 ;
;(2)由题意,
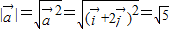 ,①
,①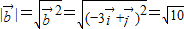 ,②
,②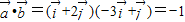 ③…(10分)
③…(10分)∵
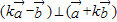 ,
,∴
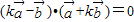 ,得,
,得,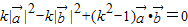
将①②③代入得:k2+5k-1=0,…(12分)
解得
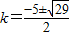 …(14分)
…(14分)点评:本题考查向量共线、垂直的条件的运用,考查数量积公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目