题目内容
已知函数
，求导函数
，并确定
的单调区间．
【答案】
当
时增区间
，减区间
；
当
时增区间
，减区间
；
当
时减区间.
【解析】本试题主要考查了含有参数的二次不等式的求解运用。首先确定定义域，然后求解导数，然后得到关于含有参数的一元二次函数，然后对于判别式记性分类讨论，确定不等式的解集，从而求解得到单调区间。当时增区间，减区间
当时增区间，减区间
当时减区间
解：因为
当时增区间，减区间
当时增区间，减区间
当时减区间
练习册系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
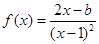，求导函数
，并确定
的单调区间．
，求导函数
，并确定
的单调区间．
，求导函数
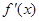，并确定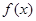
的单调区间．
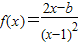，求导函数f'（x），并确定f（x）的单调区间．