题目内容
(12分)已知函数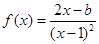
，求导函数
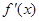，并确定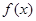
的单调区间．
【答案】
．
令
，得
．
当
，即
时，
的变化情况如下表：
|
|
|
|
|
|
|
|
|
0 |
|
|
当
，即
时，的变化情况如下表：
|
|
|
|
|
|
|
|
|
|
0 |
|
所以，当时，函数
在
上单调递减，在
上单调递增，
在
上单调递减．
当时，函数在
上单调递减，在
上单调递增，在
上单调递减．
当
，即
时，
，所以函数在上单调递减，在上单调递减．
【解析】略
练习册系列答案
名校课堂系列答案
相关题目
的部分图象如图所示.(Ⅰ) 求函数
的解析式；
的图象通过适当的变换得到函数
的定义域为集合A, 
的值域为集合B.
,求
；
,求实数
的取值范围。
的导函数
,数列
的前
项和为
,点
均在函数
的图象上．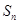
的最大值;
,其中
,求
的前
是偶函数.
有解，求m的取值范围.