题目内容
22.已知函数(Ⅰ)用![]() 表示
表示![]() ;
;
(Ⅱ)若![]() ,记
,记![]() ,证明数列
,证明数列![]() 成等比数列,并求数列
成等比数列,并求数列![]() 的通项公式;
的通项公式;
(Ⅲ)若![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,证明:
项和,证明:![]()
本题综合考察数列、函数、不等式、导数应用等知识,以及推理论证、计算及解决问题的能力。
解:(Ⅰ)由题可得![]()
所以过曲线上点![]() 的切线方程为
的切线方程为![]() ,
,
即![]()
令![]() ,得
,得![]() ,即
,即![]()
显然![]() ∴
∴![]()
(Ⅱ)由![]() ,知
,知 ,同理,
,同理,
故
从而![]() ,即
,即![]()
所以,数列![]() 成等比数列,故
成等比数列,故![]() ,
,
即![]() ,从而
,从而![]()
所以
(Ⅲ)由(Ⅱ)知
∴![]()
∴
当![]() 时,显然
时,显然![]()
当![]() 时,
时,![]() ,
,
∴![]()
![]()

![]()
综上,![]()

练习册系列答案
相关题目
 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数. 表示
表示 ;
; ,若
,若 ,试证明数列
,试证明数列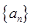 为等比数列,并求数列
为等比数列,并求数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前 ,求
,求 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数. 表示
表示 ;
; ,若
,若 ,试证明数列
,试证明数列 为等比数列,并求数列
为等比数列,并求数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前 ,求
,求